Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет 2.
|
|
Исходные данные
| СА0 | k1 | k2 | n |
| 0, 3 | 0, 05 | 0, 0075 | |
| моль/дм3 | дм3 · моль–1 · мин–1 | дм3 · моль–1 · мин–1 |
y′ = f(xi, yi)0, 05·0=, 3·е-0, 05·t -0, 0075·CP
Дополнительные расчеты
| интервал | число разбиений | |
| а | в | h |
| 47, 5 | 0, 625 |
В таблицу расчетов (табл.5.4) вносим ссылки на исходные данные.
Таблица 5.4.
Решение уравнения усовершенствованным методом Эйлера. Расчет 2.
| i | хi | yi | y′ =f(xi, yi) | xi+1/2 = хi+h/2 | yi+1/2=yi+ h/2·f(x, y) | y′ i+1/2=f(xi+1/2, yi+1/2) | h· y′ i+1/2 |
| 0, 208471 | 0, 000466498 | 40, 3125 | 0, 208617 | 0, 000435026 | 0, 000271891 | ||
| 40, 625 | 0, 208743 | 0, 000402002 | 40, 9375 | 0, 208868 | 0, 000371497 | 0, 000232186 | |
| 41, 25 | 0, 208975 | 0, 000339724 | 41, 5625 | 0, 209081 | 0, 000310159 | 0, 000193849 | |
| 41, 875 | 0, 209169 | 0, 000279597 | 42, 1875 | 0, 209256 | 0, 000250941 | 0, 000156838 | |
| 42, 5 | 0, 209326 | 0, 000221553 | 42, 8125 | 0, 209395 | 0, 000193778 | 0, 000121111 | |
| 43, 125 | 0, 209447 | 0, 000165526 | 43, 4375 | 0, 209498 | 0, 000138606 | 8, 66288E-05 | |
| 43, 75 | 0, 209533 | 0, 000111454 | 44, 0625 | 0, 209568 | 8, 53619E-05 | 5, 33512E-05 | |
| 44, 375 | 0, 209587 | 5, 92745E-05 | 44, 6875 | 0, 209605 | 3, 39855E-05 | 2, 12409E-05 | |
| 0, 209608 | 8, 92921E-06 | 45, 3125 | 0, 209611 | -1, 5582E-05 | -9, 7386E-06 | ||
| 45, 625 | 0, 209598 | -3, 964E-05 | 45, 9375 | 0, 209586 | -6, 3396E-05 | -3, 9623E-05 | |
| 46, 25 | 0, 209559 | -8, 6488E-05 | 46, 5625 | 0, 209531 | -0, 00010951 | -6, 8446E-05 | |
| 46, 875 | 0, 20949 | -0, 00013167 | 47, 1875 | 0, 209449 | -0, 00015399 | -9, 6242E-05 | |
| 47, 5 | 0, 209394 | -0, 00017524 | 47, 8125 | 0, 209339 | -0, 00019687 | -0, 00012304 |
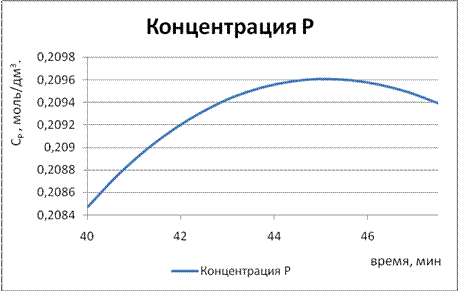
Рисунок 5.2. - Определение максимальной концентрации компонента Р для последовательной реакции по усовершенствованному методу Эйлера. Расчет 2.
Ответ: Максимальная концентрации компонента Р 0, 210 моль/дм3 достигается на 45 минуте.
Метод Рунге – Кутта.
Последовательность вычислений по методу Рунге – Кутта следующая:
1. Разобьем отрезок [a, b], на n равных частей точками хi = х0 + i · h (i = 0, 1, 2, …, n), где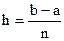 
, x0 = а, xn = b.
2. Находим для каждого i (i = 0, 1, 2, …, n) значения
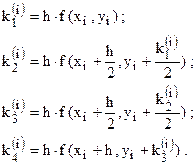
3. Вычисляем
4. Определяем последовательность значений yi (i = 0, 1, 2, …, n) искомой функции y = y (x):
yi+1 = yi + ∆ yi
Для выполнения вычислений по методу Рунге – Кутта удобно пользоваться следующей схемой.
| i | х | y | y′ = f(x, y) | k = h · f(x, y) | ∆ y |
| х0 | y0 | f(x0 , y0) | ki(0) | k1(0) | |
| х0 + h/2 | y0 + k1(0)/2 | f(x0 + h/2, y0 + k1(0)/2) | k2(0) | 2·k2(0) | |
| х0 + h/2 | y0 + k2(0)/2 | f(x0 + h/2, y0 + k2(0)/2) | k3(0) | 2·k3(0) | |
| х0 + h | y0 + k3(0) | f(x0 + h, y0 + k3(0)) | k4(0) | k4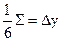(0) | |
 0
| |||||
| х1 | y = y0 + ∆ y0 | f(x1 , y0) | k1(1) | k1(1) | |
| х1 + h/2 | y1 + k1(1)/2 | f(x1 + h/2, y1 + k1(1)/2) | k2(1) | 2·k2(1) | |
| х1 + h/2 | y1 + k2(1)/2 | f(x1 + h/2, y1 + k2(1)/2) | k3(1) | 2·k3(1) | |
| х1 + h | y1 + k3(1) | f(x1 + h, y1 + k3(1)) | k4(1) | k4(1) | |
| |||||
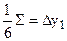
| х2 | y2 = y1 + ∆ y1 |
Метод Рунге – Кутта является одним из методов повышенной точности и, несмотря на его трудоёмкость, широко используется при численном решении дифференциальных уравнений и систем обыкновенных дифференциальных уравнений.
Пример 3. Решим уравнений (1) с начальным условием y(0) = 0 на отрезке [0, 3] с шагом h = 1.
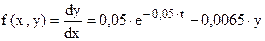
Интегрирование дифференциального уравнения методом Рунге – Кутта.
| i | х | y | y′ = f(x, y) | k = h · f(x, y) | ∆ y |
| 0, 05 | 0, 05 | 0, 05 | |||
| 0, 5 | 0, 025 | 0, 0486 | 0, 0486 | 0, 0972 | |
| 0, 5 | 0, 0243 | 0, 0486 | 0, 0486 | 0, 0972 | |
| 1, 0 | 0, 0486 | 0, 0473 | 0, 0473 | 0, 0473 | |
| 0, 0486 | |||||
| 1, 0 | 0, 0486 | 0, 0473 | 0, 0473 | 0, 0473 | |
| 1, 5 | 0, 0722 | 0, 0459 | 0, 0459 | 0, 0818 | |
| 1, 5 | 0, 0716 | 0, 0459 | 0, 0459 | 0, 0818 | |
| 2, 0 | 0, 0945 | 0, 0446 | 0, 0446 | 0, 0446 | |
| 0, 0459 | |||||
| 2, 0 | 0, 0945 | 0, 0446 | 0, 0446 | 0, 0446 | |
| 2, 5 | 0, 1168 | 0, 0433 | 0, 0433 | 0, 0966 | |
| 2, 5 | 0, 1161 | 0, 0433 | 0, 0433 | 0, 0866 | |
| 3, 0 | 0, 1378 | 0, 0421 | 0, 0421 | 0, 0421 | |
| 0, 0433 | |||||
| 3, 0 | 0, 1378 |
Ход работы:
1. Получить индивидуальное задание для расчёта кинетических кривых последовательной реакции первого порядка (СА нач., k1, k2, время протекания реакции).
2. Выполнить расчёт по приведённым схемам.
3. Построить кинетические кривые в Excel или Word.
4. Сделать вывод о точности методов.
5. Оформить отчёт в Word (А – 5).