
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции сложного процента
|
|
1.1 Накопленная сумма денежной единицы
Накопленная сумма денежной единицы (будущая стоимость единицы) - первая функция денег.
Экономический смысл данной функции состоит в том, что бы показать, какая сумма будет накоплена на счете к концу определенного периода при заданной ставке дохода, если сегодня положить на счет одну денежную единицу.
Расчеты по этой функции основываются на " простом" и " сложном" процентах.
Простой процент - приращение дохода на вложенную сумму денег по единой процентной ставке в течение всего срока инвестиции или кредита.
Сложный процент - приращение дохода на вложенную сумму денег по сумме остатка предыдущего периода времени в течение срока инвестиций или кредита.
Расчет простого процента:
 ;
;
Расчет сложного процента:
 ,
,
где:
FV – будущая стоимость;
PV – текущая стоимость, (у.е.);
i - ставка процента (%);
n - период (срок) вклада, лет.
При более частом вложении чем 1 раз в год
 , где
, где
n – число лет;
i – ставка дохода на капитал;
k – число начислений процентов в год;
(1+i)n – фактор накопленной суммы (будущей стоимости) денежной единицы при ежегодном начислении процентов;
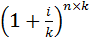 - фактор накопленной суммы (будущей стоимости) денежной единицы при более частом, чем 1 раз в год начислении процентов.
- фактор накопленной суммы (будущей стоимости) денежной единицы при более частом, чем 1 раз в год начислении процентов.
Таблица 1. Получение простого и сложного процента
| Год | Операции | Процент | |
| простой | сложный | ||
| Депозит | |||
| Получен процент Остаток на конец года | |||
| Получен процент Остаток на конец года | |||
| Получен процент Остаток на конец года | 12, 10 133, 10 | ||
| Получен процент Остаток на конец года | 13, 31 146, 41 | ||
| Получен процент Остаток на конец года | 14, 64 161, 05 |
Правило 72-х:
Применяется для примерного расчета количества лет, необходимых для увеличения денежной суммы в 2 раза:
 или
или 
Задача № 1
Условие: Определить какая сумма будет накоплена на счете к концу 24, 5-го года, если сегодня внести на счет, приносящий 12 % годовых, 3750 руб.
Решение:
1. Начисление процента осуществляется в конце каждого года
FV = 3750*(1+0, 12) 24, 5 = 60238, 32 руб.
2. Начисление процента осуществляется в конце каждого месяца
FV = 3750*(1+0, 12/12) 24, 5*12 = 3750*15, 31=57423 руб.
1.2 Текущая стоимость единицы
Текущая стоимость единицы - вторая функция денег.Применяется в оценке текущей стоимости тех денег, которые могут быть получены в конце определенного периода. Экономический смысл – данная функция показывает какова при заданной ставке дисконта текущая стоимость одной денежной единицы, получаемая в конце определенного периода времени.
Определяется по формулам:
1. при начислении процентов 1 раз в год
 ;
;
 ;
;
где:
PV - настоящий платеж, руб;
FV - будущий платеж (Кn), руб;
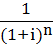 - фактор текущей стоимости единицы, при ежегодном начислении процентов;
- фактор текущей стоимости единицы, при ежегодном начислении процентов;
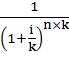 – фактор текущей стоимости единицы при более частом, чем 1 раз в год начислении процентов.
– фактор текущей стоимости единицы при более частом, чем 1 раз в год начислении процентов.
Задача № 2
Условие: Определить текущую стоимость 3800 руб., которые
были бы получены в конце 7 года при 23% ставке дисконта.
При условиях:
начисление ежеквартально;
Решение:
РV=3800* 1/(1+0, 23 / 12)7*12 = 3800*1/(1, 091)84 = 3800*1/4, 927 = 3800*0, 2029 = 771, 260 руб.
1.3 Накопление денежной единицы за период
Накопление денежной единицы за период или текущая стоимость единицы реверсии -третья функция денег.Экономический смысл функции – показывает, какая сумма будет накоплена на счете при заданной ставке, если регулярно в течение определенного периода откладывается на счет одна денежная единица.
Определяется по формулам:
Расчет будущей стоимости обычного аннуитета (платежи в конце периода):
 ;
;
 ;
;
где:
РМТ – равновеликие периодические платежи (поступления);
k - количество начислений в год (период);
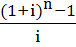 – фактор накопления денежной единицы за период при платежах, осуществляемых 1 раз в конце года;
– фактор накопления денежной единицы за период при платежах, осуществляемых 1 раз в конце года;
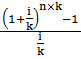 – фактор накопления денежной единицы за период при платежах, осуществляемых чаще, чем 1 раз в год в конце каждого периода.
– фактор накопления денежной единицы за период при платежах, осуществляемых чаще, чем 1 раз в год в конце каждого периода.
Авансовые платежи (платежи производятся в начале периода):
 ;
;
 ;
;
где:
РМТ – равновеликие периодические платежи (поступления);
k - количество начислений в год (период);
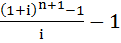 – фактор накопления денежной единицы за период при платежах, осуществляемых 1 раз в начале года;
– фактор накопления денежной единицы за период при платежах, осуществляемых 1 раз в начале года;
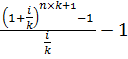 – фактор накопления денежной единицы за период при платежах, осуществляемых чаще, чем 1 раз в год в начале каждого периода.
– фактор накопления денежной единицы за период при платежах, осуществляемых чаще, чем 1 раз в год в начале каждого периода.
Задача № 3
Условие: Определить сумму, которая будет накоплена на счете приносящем 20% годовых к концу 35 месяца, если откладывать в начале и в конце каждого полугодия на счет 4900 рублей.
а) платежи в конце полугодия;
б) платежи в начале полугодия;
Решение:
а) FV = 4900*((1+0, 20/2)2, 92*2 –1)/0, 20/2 = 36492, 76 руб.
б) FV = 4900* (1, 91922-1/0, 1-1) = 4900*8, 1922=40142, 04 руб.
1.4 Формирование фонда возмещения
Формирование фонда возмещения - четвертая функция денег.
Используется для расчета равновеликих периодических платежей, которые необходимо осуществлять в течении определенного периода для того, чтобы к концу срока иметь на счете запланированную сумму денег. Экономический смысл функции – показывает, сколько нужно откладывать на счет регулярно в течение определенного времени, чтобы при заданной ставке дохода иметь на счете к концу этого срока одну денежную единицу.
Определяется по формулам:
 ;
;
 ;
;
где:
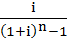 - фактор фонда возмещения при платежах, осуществляемых 1 раз в год;
- фактор фонда возмещения при платежах, осуществляемых 1 раз в год;
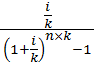 – фактор фонда возмещения при платежах, осуществляемых чаще, чем 1 раз в год.
– фактор фонда возмещения при платежах, осуществляемых чаще, чем 1 раз в год.
Задача № 4
Условие: Определить сумму платежей, чтобы к концу 5-го года
иметь на счете, приносящем 22% годовых, 64 000 руб.
При условиях:
а) начисление ежемесячно;
б) начисление ежедневно.
Решение:
а) PMT=64000* (0, 22/12)/(1+0, 22/12)5*12-1)= 594, 35 руб.
б) PMT=64000* (0, 22/365)/(1+0, 22/365)5*365-1)= 19, 31 руб.
1.5 Взнос на амортизацию
Взнос на амортизацию- пятая функция денег. Данная функция используется для определения обязательных периодических платежей, необходимых для погашения (возврата) кредита в течении установленного срока. Экономический смысл функции – показывает, какими должны быть аннуитетные (равновеликих, регулярных) платежи в счет погашения кредита в одну денежную единицу, выданного на определенный период при заданной ставке процента по кредиту.
Определяется по формулам:
а) при платежах осуществляемых 1 раз в год
 ;
;
б) при платежах, осуществляемых чаще чем 1 раз в год
 ;
;
где:
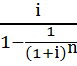 – фактор взноса на амортизацию единицы при платежах, осуществляемых 1 раз в год;
– фактор взноса на амортизацию единицы при платежах, осуществляемых 1 раз в год;
 - фактор взноса на амортизацию единицы при платежах, осуществляемых чаще, чем 1 раз в год.
- фактор взноса на амортизацию единицы при платежах, осуществляемых чаще, чем 1 раз в год.
Задача № 5
Условие: Кредит в размере 275 000 рублей выдан на 15 лет под 19% годовых. Определить размер аннуитетных платежей.
Погашение кредита осуществляется в конце каждого месяца
Решение:
РМТ=275 000*(0, 19/12)/(1-1/(1+0, 19/12)15*12)=4627, 08 руб.
1.6 Текущая стоимость аннуитета
Текущая стоимость аннуитета - шестая функция денег. Используется для того, чтобы определить текущую стоимость регулярных платежей, получаемых в будущем в течение определенного времени. Экономическийсмысл функции – определить, какова при заданной ставке дисконта текущая стоимость серии равновеликих платежей в одну денежную единицу, поступающих в течение определенного периода.
Расчет текущей стоимости обычного аннуитета (платежи производятся в конце периода):
а). при платежах, осуществляемых 1 раз в конце периода:
 ,
,
б). при платежах, осуществляемых чаще, чем 1 раз в год в конце каждого периода:
 ,
,
где:
PMT - равновеликие периодические поступления, руб;
 - фактор текущей стоимости аннуитета при платежах, осуществляемых 1 раз в конце года;
- фактор текущей стоимости аннуитета при платежах, осуществляемых 1 раз в конце года;
 - фактор текущей стоимости аннуитета при платежах, осуществляемых чаще, чем 1 раз в год в конце каждого периода.
- фактор текущей стоимости аннуитета при платежах, осуществляемых чаще, чем 1 раз в год в конце каждого периода.
Расчет текущей стоимости авансового аннуитета (платежи производятся в начале периода):
а). при платежах, осуществляемых 1 раз в начале года:
 ,
,
б). при платежах, осуществляемых чаще, чем 1 раз в год в начале каждого периода:
 ,
,
где:
PMT - равновеликие периодические поступления, руб.;
(1-1/(1+i)n-1)/i+1 – фактор текущей стоимости аннуитета при платежах, осуществляемых 1 раз в начале года;
(1-1/(1+i/k)n*k-1)/i/k+1 – фактор текущей стоимости аннуитета при платежах, осуществляемых чаще, чем 1 раз в год в начале каждого периода.
Задача № 6
Условие: Договор аренды квартиры составлен на 12 месяцев. Определить текущую стоимость арендных платежей при 22% ставке дисконтирования. Арендная плата 1850 руб.
При условиях:
а) в конце каждого месяца;
б) в начале каждого месяца.
Решение:
а). PV = 1850*(1-1/(1+0, 22/1)1*12)/0, 22 = 7635, 62 руб.
б). PV = 1850*(1-1/(1+0, 22/1)1*12-1)/0, 22/1+1= 9315, 51 руб.