
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сведения из теории
|
|
Лабораторная работа 1
Формирование случайных величин с заданными статистическими характеристиками.
Цель работы:
- изучение методов формирования одномерной случайной величины с заданным законом распределения вероятностей;
- получение массива случайных величин для дальнейшей обработки;
- изучение методов формирования двумерной случайной с заданными числовыми характеристиками;
Сведения из теории
Непременным этапом проектирования производственных систем является моделирование их поведения уже на стадии эскизного проектирования. На этой же стадии производится расчет надежности с целью прогнозирования ожидаемых показателей надежности. При моделировании систем, находящихся под воздействием случайных величин, случайных потоков и случайных процессов очень часто приходится формировать случайные величины и процессы с заданными статистическими характеристиками.
Формирование случайных величин с заданными законами распределения.
Случайные числа с заданными законами распределения, как правило, получают с помощью специальных подпрограмм. Алгоритмическая основа состоит в следующем. Пусть f(x) - функция плотности вероятности случайной величины x;
F(x) = 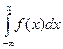 - функция вероятности этой случайной величины. Значения функции распределения лежат в интервале 0 - 1.
- функция вероятности этой случайной величины. Значения функции распределения лежат в интервале 0 - 1.
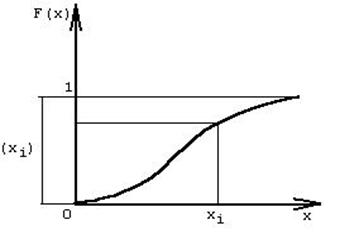
Рис. 1
Из рис.1 видно, что любому значению xi соответствует значение функции F(xi). Если в интервале 0 - 1 формировать значения F(x) по равномерному закону распределения, то для каждого значения F(x) по графику можно определить соответствующее значение xi. Закон распределения случайных чисел xi будет соответствовать функции F(x). Задача может быть решена аналитически, если аналитически задана требуемая функция распределения F(x) или функция плотности распределения. Таким образом, идея изложенного метода состоит в формировании равномерно - распределенной случайной величины с дальнейшим нелинейным преобразованием равномерного распределения.
Последовательность решения этой задачи следующая:
1) Формируется равномерно распределенная случайная величина в диапазоне 0 - 1
2) Записывается заданный закон распределения:
ξ = F(x) = ∫ f(x)dx
3) Для каждого значения ξ i равномерной случайной величины определяется значение xi