Свойства функции Лапласа

Нормальное распределение. Его числовые характеристики. Ассиметрия и эксцесс.

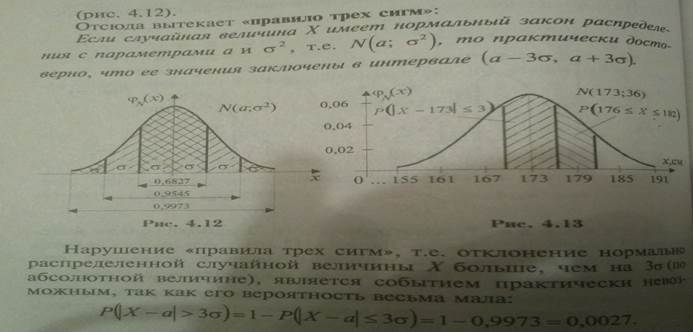
Функция Лапласа и его св-ва. Правило 3 сигм.

Функция Лапласа.

Функция Лапласа используется для вычисления вероятностей нормального распределения.

Свойства функции Лапласа

1) Ф(0) = 0;

2) Ф(- х) = - Ф(х);

3) Ф(¥) = 1.

18. Случайная величина Х имеет равномерное распределение на интервале [a; b], если на этом интервале плотность вероятности случайной величины Х постоянна, а вне его равна нулю, т.е., если

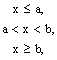
где с - постоянная величина (c=const). Равномерное распределение иногда называют законом равномерной плотности.

Свойства математических ожиданий:

1. Математическое ожидание постоянной величины равно этой постоянной; т.е. если С-постоянная величина, то

М(С) = С.

2. Постоянный множитель можно выносить за символ математического ожидания, т.е. если k постоянный множитель, то

М(kX) = k*M(X)

3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е.

M(X+Y) = M(X)+M(Y)

4. Математическое ожидание разности случайных величин равно разности их математических ожиданий, т.е.

M(X-Y) = M(X)-M(Y)

Математическое ожидание произведения случайных величин равно произведению их математических ожиданий, т.е.

M(X*Y) = M(X)*M(Y)

6. Если все значения случайной величины увеличить (уменьшить) на одно и тоже число С, то ее математическое ожидание увеличится (уменьшиться) на это же число

M(X+-C) = M(X)+-C

б) дисперсией D(X) случайной величины Х называется математического ожидания α (M(X)= α:

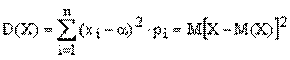
в) средним квадратическим отношением G(X) (G) случайной вершины называется арифметическим значением корня квадратного из дисперсии, т.е.
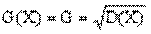