Вместо задачи 2.6

Найти приближенное решение начально-краевой задачи для уравнения теплопроводности:

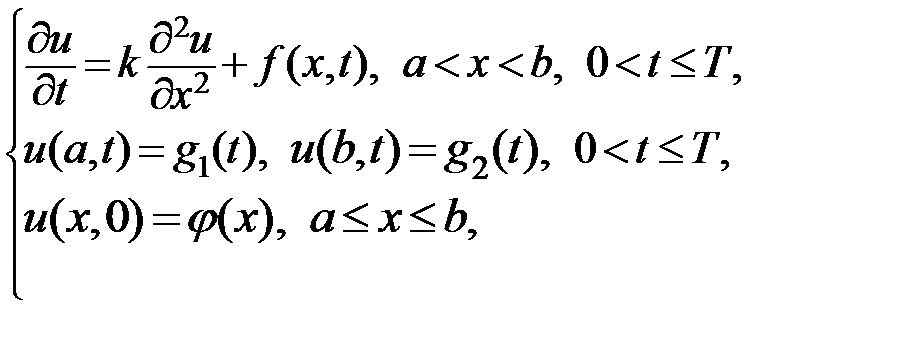
используя явную разностную схему. Взять 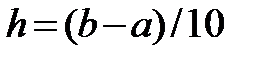; шаг 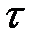выбрать из условия устойчивости. Изобразить графики зависимости приближенного решения от 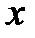при t= 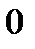, , 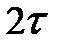, 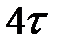… T.

УКАЗАНИЕ. Условие устойчивости для явной разностной схемы имеет вид .

Таблица к задаче 22

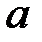
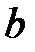
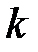
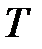
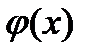
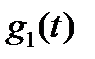
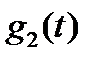
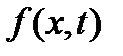
				0.05				x
	-1		0.5	0.4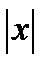
			0.1	0.5	x (1 -x)	5 t	5 t
				0.2				x
			0.1	0.5	x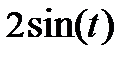
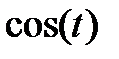
	-1			0.1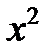
				0.02				x (1 -x)
	-1		0.5	0.4		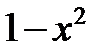		x
			0.1	0.5		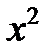		t
	-1		0.2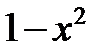
				0.05		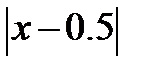0.5	0.5
	-1		0.5	0.4		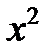		x
			0.2	0.25
				0.2
				0.05
				0.2
			0.5	0.1
			0.5	0.4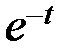
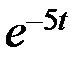
			0.2	0.2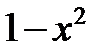
				0.1			10 t
			0.5	0.1			10 t	t
				0.2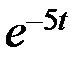
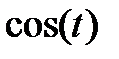
			0.4	0.1	x
	-1			0.2		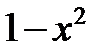	5 t
			0.4	0.1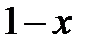
				0.2	x			x
			0.25	0.2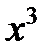
				0.2	x			x
			0.5	0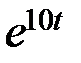.1			-1
	-1		0.2		1-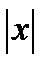

Л.Р. 2.2.

Аппроксимации граничных условий второго рода в методе конечных разностей

.

Оглавление

1. Введение

1.1. Постановка задачи

1.2. Способы реализации ГУ второго рода

2. Краткое описание программы

2.1. Возможности программы

3. Практическая часть

4. Отчёт

1. Введение

Цель работы - знакомство с наиболее часто применяемыми способами аппроксимации граничных условий второго рода (граничных условий Неймана) в методе конечных разностей (на примере ГУ для одномерного нестационарного уравнения теплопроводности).

1.1. Постановка задачи

Задачи, которые будут использоваться для анализа свойств численных решений с ГУ второго рода, формулируются так: в стержне длиной L с теплоизолированной боковой поверхностью торец x= 0 поддерживается при постоянной температуре T ₀ (ГУ первого рода), а торец x= 1– теплоизолирован (ГУ второго рода); температуропроводность материала стержня постоянна и равна a; в начальный момент времени t= 0 стержень нагрет до температуры T _нач(x) (координата x отсчитывается от левого торца стержня; см. рис.1). Найти распределение температуры по стержню в любой момент времени, т.е. найти функцию T (x, t) для 0< x ≤ L и t> 0.

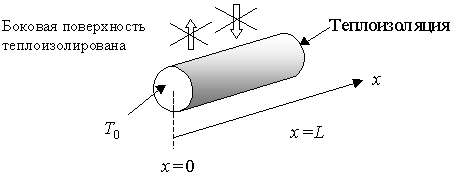
Рис. 1. Система координат и обозначения. (Стержень круглого сечения нарисован условно – сечение может иметь любую форму и если боковая поверхность теплоизолирована, то температура любой точки стержня может зависеть только от координаты x и не будет зависеть от координаты поперек стержня).

Искомая функция T (x, t) является решением одномерного уравнения теплопроводности, которое в безразмерных координатах имеет вид:

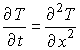
(См. описание работы Л Р.1 .2; в дальнейшем ссылка на него будет обозначаться Л Р.1).

Граничные условия:

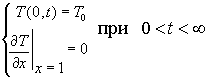
(на границе x= 0 граничное условие первого рода, а при x= 1 – второго).

Начальные условия: T (x, 0)= T _нач(x)при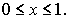

1.2. Способы реализации ГУ второго рода

Методы конечных разностей, применяемые для численного решения задач с граничными условиями второго (и третьего) рода, не имеют никаких принципиальных отличий от методов, применяемых для задач с ГУ первого рода. Для решения поставленной задачи методом конечных разностей необходимо представить граничное условие второго рода в " естественном" для этого метода виде, т.е. с использованием численного решения (величин 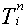). Иными словами, производную в граничном условии надо заменить её разностной аппроксимацией, а это можно сделать многими способами.

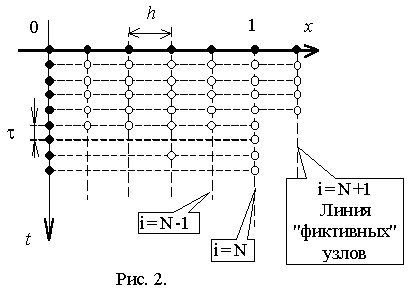
Рассмотрим только два способа реализации ГУ второго рода, которые будут использованы в расчётах. При рассмотрении используем ту же равномерную сетку, что и в Л Р.1 (показана на рис.2). Первый способ. Приближенно значение производной при x= 1 можно записать, используя аппроксимацию производной по x левой разностью:

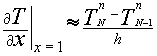
(1)

а поскольку значение этой производной в рассматриваемой задаче равно нулю, то аппроксимация граничного условия выглядит так:

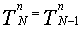
(2)

Численное решение ДУ с граничным условием второго рода при x= 1
происходит почти так же, как и с ГУ первого рода: на каждом шаге по времени с помощью разностной схемы вычисляются все 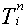при 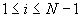, а значение 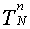(на границе) вычисляется по формуле (2). Это и есть первый способ реализации граничного условия второго рода.

Обратите внимание на то, что разностная аппроксимация первой производной левой разностью (ф-ла (1)) имеет первый порядок точности по h, т.е. O (h).

Второй способ можно пояснить на примере явной разностной схемы аппроксимации уравнения теплопроводности. Алгоритм явной схемы можно записать так:

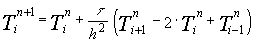
(3)

Из этого выражения следует, что для вычисления величины 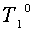требуется какая-то величина 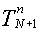, которая не входит в расчетную область. Однако её можно вычислить, используя аппроксимацию производной в граничном условии центральной разностью:

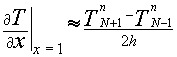
(4)

а поскольку значение этой производной в рассматриваемой задаче равно нулю, то аппроксимация граничного условия выглядит так:

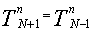
(5)

Способ реализации граничного условия здесь несколько иной: на каждом шаге по времени с помощью разностной схемы вычисляются все 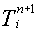при 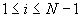, а при вычислении 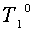в разностной схеме заменяются 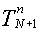на 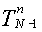(используется равенство (5)).

Обратите внимание на то, что разностная аппроксимация первой производной центральной разностью (ф-ла (4)) имеет второй порядок точности по h, т.е. O (h ²).

Рассмотренному выше второму способу реализации ГУ второго рода можно дать другую интерпретацию, которая может оказаться более наглядной и полезной в сложных задачах. Эта другая интерпретация связана с введением " фиктивных" узлов (узлов вне зоны расчета). На рис.2 показаны такие узлы (линия узлов, находящихся на расстоянии h от границы, на которой поставлено ГУ второго рода). Если температуру в этих узлах задавать равной значениям температуры в соответствующих симметричных относительно границы узлах (согласно равенству (5)), то для расчета будет использоваться одна и та же разностная схема для всех узлов (включая и узлы при i=N).

2. Краткое описание программы

2.1. Возможности программы

В работе должна быть предусмотрена возможность численного решения уравнения теплопроводности с помощью неявной и явной разностных схем. Возможность использования различных граничных и начальных условий ограничена задачами, которые позволяют в достаточной мере познакомиться с основными способами реализации ГУ второго рода и их свойствами.

Шаги сетки выбираются аналогично Л Р.1. Расчетная область по времени, реализованная в программе, составляет во всех случаях [0, 1]. Результаты расчета выводятся в виде такой же как и в Л Р.1таблицы. После расчета программа может построить такие же как в Л Р.1 графики.

1. Практическая часть

ЗАДАНИЕ. Найти приближенное решение начально-краевой задачи для уравнения теплопроводности:

.

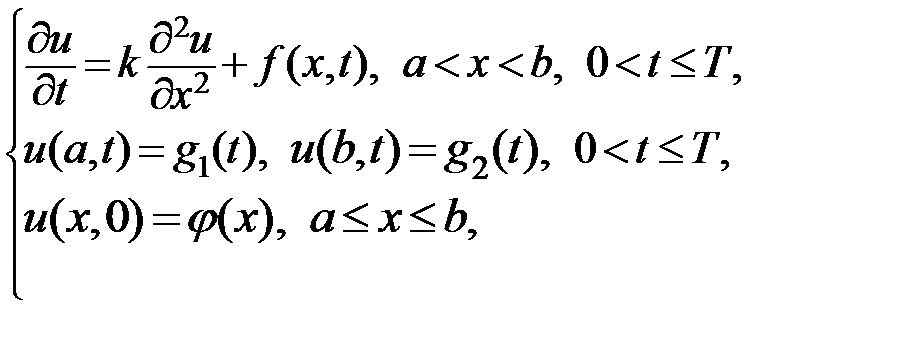используя явную и неявную разностные схемы. Изобразить графики зависимости приближенного решения от 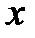при t= 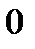, , 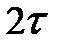, 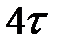… T.

Таблица 1

№
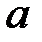
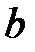
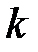
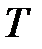
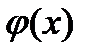
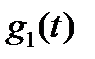
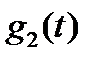
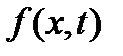
				0.05				x
	-1		0.5	0.4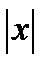
			0.1	0.5	x (1 -x)	5 t	5 t
				0.2				x
			0.1	0.5	x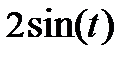
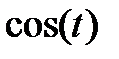
	-1			0.1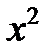
				0.02				x (1 -x)
	-1		0.5	0.4		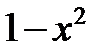		x
			0.1	0.5		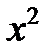		t
	-1		0.2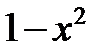
				0.05		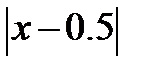0.5	0.5
	-1		0.5	0.4		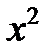		x
			0.2	0.25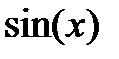
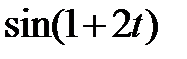
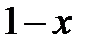
				0.2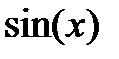
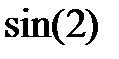
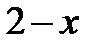
				0.05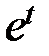
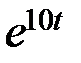
				0.2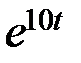
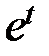
			0.5	0.1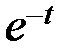
			0.5	0.4
			0.2	0.2
				0.1			10 t
			0.5	0.1			10 t	t
				0.2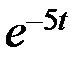
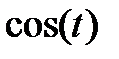
			0.4	0.1	x
	-1			0.2		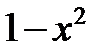	5 t
			0.4	0.1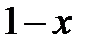
				0.2	x			x
			0.25	0.2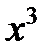
				0.2	x			x
			0.5	0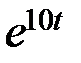.1			-1
	-1		0.2		1-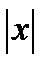

УКАЗАНИЕ. Условие устойчивости для явной разностной схемы имеет вид .

• Для обеих разностных схем выполните расчеты, результаты которых позволят определить порядок сходимости для первого способа реализации ГУ второго рода. Результаты расчетов для каждой схемы запишите в таблицу вида:

В двух первых колонках – задаваемые Вами параметры сетки, а в остальных – числа из таблиц результатов расчета. Учтите замечания, приведенные в описания Л Р.1

• Кроме указанных расчетов, дополнительно сделайте такие же расчеты для явной схемы при выполнении соотношения t = h ²/6.

• По результатам всех расчетов определите порядки сходимости по h и t применённых разностных схем. Постройте в логарифмическом масштабе графики зависимостей ошибки численных решений от h или t. (Пример – рис.5 в Л Р.1).

• Повторите все предыдущие расчёты и задания для аппроксимации ГУ второго рода вторым способом.

Обратите внимание на то, как сильно влияет на точность решения понижение порядка точности аппроксимации лишь в одном (граничном) узле сетки. (Вспомните, что и явная и неявная схемы имеют второй порядок сходимости по h).

По результатам всех этих расчетов проанализируйте влияние порядка точности аппроксимации ГУ второго рода на порядок сходимости.

4. Отчёт

В отчёте должны быть таблицы расчётов (их вид в разделе 3), построенные Вами графики для определения порядка сходимости и сделаны соответствующие выводы о свойствах применённых способов аппроксимации ГУ второго рода (с точки зрения их влияния на порядок сходимости и точность численного решения).

Литература

1. Андерсон Д., Таннехилл Дж., Плетчер Р. Вычислительная гидромеханика
и теплообмен. Пер. с англ.: В двух томах. -М.: Мир, 1990. -728 с.

2. Флетчер К. Вычислительные методы в динамике жидкостей. Пер. с англ.
В двух томах. -М.: Мир, 1991. -504+552 с.

3. Оран Э., Борис Дж. Численное моделирование реагирующих потоков. Пер. с англ. -М., Мир, 1990. -660 с.

4. Роуч П. Вычислительная гидродинамика. Пер. с англ. -М.: Мир, 1980. -616 с.