Теоретическое описание

Лабораторная работа № 3.12

ИНТЕРФЕРЕНЦИЯ

Задание 1. ОПЫТ ЮНГА

ЦЕЛЬ РАБОТЫ: определение расстояния между щелями по интерференционной картине в схеме опыта Юнга.

Теоретическое описание

Одним из первых ученых, кто наблюдал явление интерференции, был Томас Юнг, который в 1802 году получил интерференционную картину в установке, показанной на рис.1. Свет, проходя через отверстие S в экране А, падал на экран В, в котором были проделаны две тонкие щели S ₁ и S ₂.

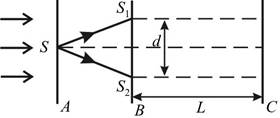
Рис. 1. Схема опыта Юнга.

Эти щели являлись когерентными источниками света и давали достаточно четкую интерференционную картину на экране С.

Схема опыта представлена на рис.2., где S ₁ и S ₂ – источники когерентного излучения, s ₁ и s ₂ – пути света от источников до точки наблюдения Р, d – расстояние между щелями, L – расстояние между экранами В и С.

Оптическая разность хода волн 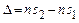, где 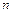– показатель преломления среды.

Если в 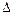укладывается целое число длин волн mλ, где m – целое число, то разность фаз оказывается кратной 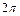, и в точке экрана будет наблюдаться интерференционный максимум.

Если в 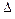укладывается нечетное число длин полуволн , то разность фаз оказывается кратной 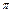, и в точке экрана будет наблюдаться интерференционный минимум.

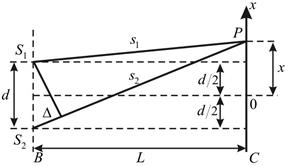
Рис. 2. Иллюстрация к явлению интерференции.

По рис.2 запишем применения теоремы Пифагора:

.

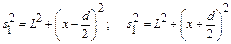Вычитая уравнения, получаем

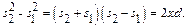
Учитывая, что 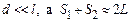и умножив последнее равенство на n, получим оптическую разность хода

.

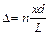Подставим в это выражение условия максимумов и минимумов интенсивности света при интерференции, получим:

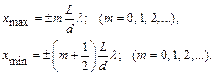
Ширина интерференционной полосы на экране будет определяться выражением

.
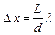