
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интерференция в воздушном зазоре. Полосы равной толщины
|
|
Пусть плоская монохроматическая волна с длиной волны 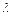 , падает на тонкий воздушный зазор толщиной d между двумя
, падает на тонкий воздушный зазор толщиной d между двумя
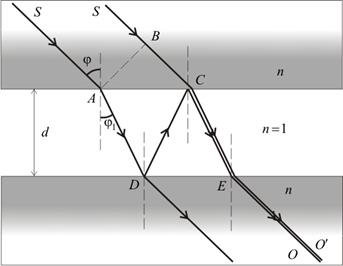
Рис. 1. Оптическая схема для наблюдения полос равной толщины.
плоскопараллельными пластинками (n – показатель преломления пластин) под углом падения φ (рис. 1). Оптическая разность хода интерферирующих лучей 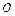 и
и 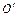 равна
равна
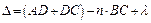 . (1)
. (1)
Дополнительная разность хода λ обусловлена отражениями от оптически более плотной среды в точках С и D (при углах 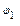 , меньших угла Брюстера, на каждом отражении сдвиг на
, меньших угла Брюстера, на каждом отражении сдвиг на 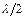 , вследствие изменения фазы волны на
, вследствие изменения фазы волны на 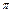 ).
).
По рис. 1 составим геометрические соотношения:
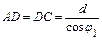 (2)
(2)
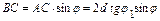 (3)
(3)
Применим закон преломления света
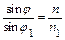 (4)
(4)
Решая систему уравнений (1) – (4) получим выражение (оптическая разность хода лучей при интерференции на тонкой пленке)
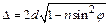 (5)
(5)
Добавив к выражению (5) условия максимумов и минимумов интенсивности света при интерференции двух когерентных волн, получаем:
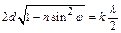 , (6)
, (6)
условия максимумов и минимумов для интерференционной картины, образуемой волнами, отраженными от обеих поверхностей в зазоре. При 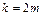 минимумы и
минимумы и 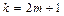 максимумы, где m – целое число.
максимумы, где m – целое число.
Пусть воздушный зазор имеет форму клина с углом α (рис. 2).
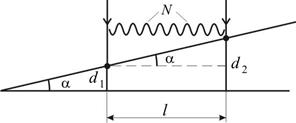
Рис. 2. Иллюстрации к явлению интерференции на тонком клине.
В прошедшем (и отраженном) свете на поверхности пластины будут наблюдаться темные и светлые интерференционные полосы. Эти полосы называются полосами равной толщины, так как каждая из них проходит через точки с одинаковыми значениями d.
Для двух лучей составим систему уравнений:
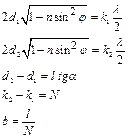 (7)
(7)
Решая систему (7) получаем выражение для ширины интерференционной полосы b (расстояния между двумя соседними минимумами):
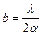 .
.
Или выражение для величины угла при вершине клина
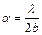 (8)
(8)