
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции расстояния
|
|
При построении правил классификации на основе функций расстояния в качестве предпосылки используется то соображение, что естественным показателем сходства образов является степень близости точек, описывающих эти образы в Евклидовом пространстве.
Рассматривая пример на рисунке 4.5, можно интуитивно отнести объект x к классу ω 1, исходя из тех соображений, что описывающая его точка располагается ближе к объектам именно этого класса, нежели к объектам класса ω 2.
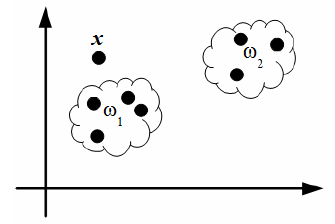
Рисунок 4.5 – Отнесение объекта к классу на основе расстояния
При использовании функций расстояния классы объектов представляются в виде кластеров в параметрическом пространстве. На этапе распознавания используется критерий минимума расстояния между точкой распознаваемого объекта и кластером класса, к которому этот объект должен быть отнесён. Построение правил классификации заключается в построении кластеров оптимальным образом.
Следует, однако, заметить, что данная методика эффективна только при наличии кластеризационных свойств у рассматриваемых классов объектов, т.е. когда расстояние между объектами внутри классов существенно меньше расстояния между группами точек, образующих классы.
Рассмотрим действие правил классификации, основанных на функциях расстояния. В некоторых случаях объекты каждого класса группируются вокруг некоторого единичного образа, являющегося типичным или репрезентативным для этого класса. В этом случае говорят, что класс представляется своим единственным эталоном. Например, такое явление наблюдается при распознавании печатных символов. В этой ситуации эффективным оказывается применение критерия минимального расстояния между распознаваемым объектом x и каждым из эталонов имеющихся классов z 1, z 2, …, z M. Расстояние между образом x и одним из эталонов z i в Евклидовом пространстве определяется как
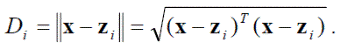 (4.6)
(4.6)
Образ зачисляется в класс ω i, если выполняется условие Di < Dj для всех j ≠ i.
Возведение (4.6) в квадрат даёт
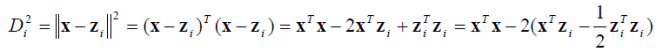 Поскольку все расстояния неотрицательны, выбор минимального расстояния Di эквивалентен выбору минимального квадрата расстояния Di 2. Однако, поскольку член x T x не зависит от номера класса i, это в свою очередь эквивалентно выбору максимального значения
Поскольку все расстояния неотрицательны, выбор минимального расстояния Di эквивалентен выбору минимального квадрата расстояния Di 2. Однако, поскольку член x T x не зависит от номера класса i, это в свою очередь эквивалентно выбору максимального значения
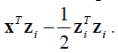
Это обстоятельство даёт набор решающих функций
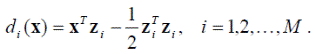
таких, что образ x относится к классу ω i, если выполняется условие di (x) = dj (x)для всех j ≠ i. Отметим, что полученные решающие функции линейны и могут быть записаны в виде
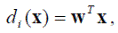
где
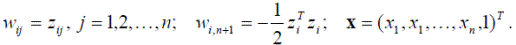
Таким образом, классификатор, действующим по принципу минимального расстояния, является частным случаем линейного классификатора. Специфическим свойством данного классификатора является то обстоятельство, что линейная разделяющая поверхность, обеспечивающая разбиение распознаваемых объектов на два класса, является гиперплоскостью, все точки которой равноудалены от эталонов этих классов. На рисунке 4.6 представлена двумерная иллюстрация разделяющей поверхности.
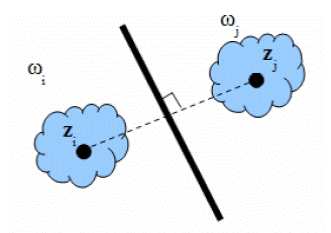
Рисунок 4.6 – Разделение классов, задаваемых одним эталоном
Иногда класс ω i может характеризоваться не единственным эталоном z i, а некоторой их группой z i 1, z i 2, …, z iNi, z i 1, где Ni — число эталонов, задающих i -й класс. В этом случае расстояние от распознаваемого образа x i до данного класса можно задать как
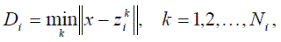
т.е. использовать наименьшее расстояние от образа до одного из эталонов. Используя это выражение, в случае множественности эталонов можно следовать описанному выше критерию минимального расстояния. При этом решающие функции будут выглядеть как
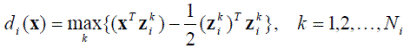
При множественности эталонов границы, разделяющие два класса, будут кусочно-линейными.
Область применения подхода, основанного на использовании критерия минимального расстояния, не исчерпывается случаями задания классов с помощью эталонов. Рассмотрим случай, когда задана выборка объектов
{ s 1, s 2, …, s N }, для каждого из которых известна принадлежность одному из классов ω 1, ω 2, …, ω M. Определим правило классификации на основе принципа ближайшего соседа (БС-правило): распознаваемый объект следует отнести к тому классу, к которому принадлежит его ближайший сосед из выборки { s i }. Ближайшим соседом образа x называется такой образ s i, для которого выполнено
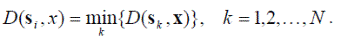
В данном случае учитывается принадлежность одному из классов только одного ближайшего соседа, вследствие чего это правило можно назвать 1-БС-правилом. Можно рассмотреть более общий случай — q-БС-правило. В этом случае для классификации образа следует определить q его ближайших соседей и отнести его к тому классу, к которому относится наибольшее число образов из получившейся группы.
Обратимся теперь к методам выявления кластеров в Евклидовом параметрическом пространстве, используемых описанными правилами классификации. Эта задача заключается в нахождении среди объектов выборки { x 1, x 2, …, x N } некоторого поднабора { z 1, z 2, …, z M }, M ≤ N, объекты которого представляют собой центры кластеров (их число соответствует числу классов), а также в отнесении всех прочих объектов к этим кластерам. В настоящее время разработано достаточно много методов выявления кластеров. Следует отметить, что, как правило, решение этой задачи носит в той или иной мере эвристический характер и зависит от рассматриваемых данных, выбранной меры близости и критерия качества кластеризации. Рассмотрим несколько простых методов выявления кластеров.
Один из простейших способов выявления кластеров заключается в следующем.
Имеется выборка { x 1, x 2, …, x N } и некоторая неотрицательная пороговая величина T. Пусть центр первого кластера совпадает с одной из точек выборки; для простоты положим z 1= x 1.
Вычисляется расстояние D 21между образом x 2и первым центром z 1. Если это расстояние больше пороговой величины T, то точка x 2назначается центром нового, второго кластера. Иначе, эта точка включается в первый кластер. Пусть, например, это условие выполнено и z 2= x 2. Далее вычисляются расстояния D 31 и D 32от точки x 3 до центров z 1и z 2. Если обе эти величины больше порога T, x 3назначается центром нового кластера. Если хотя бы одно из расстояний меньше порога, образ x 3 зачисляется в тот кластер, к центру которого он ближе. Далее, по тому же принципу, для каждого образа вычисляются расстояния от него до всех имеющихся центров, и если все эти величины превосходят порог, этот образ выделяется в отдельный кластер; в противном случае он зачисляется в кластер с ближайшим к нему центром.
Результаты его применения данного способа зависят от выбора первого центра, порядка обхода объектов выборки, величины порога T, а также геометрических свойств выборки. Однако, несмотря на эти недостатки, он эффективен с вычислительной точки зрения, т.к. выполняет только один проход по выборке.
Алгоритм максиминного расстояния.
Другим алгоритмом выявления кластеров является алгоритм максиминного расстояния. Он во многом схож с предыдущим алгоритмом, но его особенностью является стремление к выделению в первую очередь наиболее удалённых кластеров. Как и ранее, произвольный образ, например x 1, назначается первым центром z 1. Далее для всех остальных объектов вычисляется расстояние до этого центра и наиболее удалённый назначается новым центром.
На следующем шаге вычисляются пары расстояний от каждого из оставшихся объектов до двух имеющихся центров z 1и z 2и из каждой пары выбирается минимальное. После этого выбирается максимальное из полученных минимальных расстояний, и, если оно составляет значительную часть расстояния между z 1и z 2(например, не менее половины этого расстояния), соответствующий образ назначается центром z 3. Если максиминное расстояние недостаточно велико, алгоритм останавливается. На всех последующих шагах процедура повторяется с учётом нового набора кластеров. Для каждого объекта, не являющего центром, вычисляются наборы расстояний до всех имеющихся центров кластеров и в каждой группе выбирается минимальное. Максимальное среди минимальных расстояний сравнивается с «типичным» расстоянием между центрами кластеров (например, «типичным» расстоянием может служить среднее). Если это расстояние достаточно велико, образуется новый кластер, в противном случае процедура завершается. Каждый их объектов, не назначенных в качестве центров, относится к тому кластеру, центр которого к нему ближе.
Ещё один распространённый алгоритм носит название алгоритма «K -средних». Этот подход имеет формальный критерий качества, который минимизируется в процессе выполнения алгоритма: сумма квадратов расстояний от всех объектов каждого кластера до центра кластера. Ещё одним его отличием является необходимость знания требуемого числа кластеров до начала кластеризации. Алгоритм состоит из следующих шагов.
1. В исходной выборке произвольно назначаются K исходных кластеров:
z 1 (1), z 2 (1), …, z K (1).
2. На k -м шаге заданная выборка образов { x i } распределяется по K имеющимся кластерам по следующему правилу:
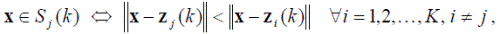
где Sj (k) — множество образов, входящих в кластер с центром в точке z j (k).
3. Определяются новые центры кластеров z j (k +1), j = 1, 2, K, исходя из минимизации показателя качества
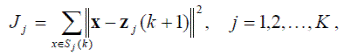
представляющего сумму квадратов расстояний от объектов кластера до его центра.
Объект z j (k +1), минимизирующий показатель качества, представляет собой, по сути, выборочное среднее по множеству Sj (K). Следовательно, новые центры кластеров можно вычислить как
z j (k) = 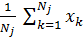 ,
,
где Nj — число образов в множестве Sj (K).
4. При выполнении условия z j (k +1) = z j (k) для всех j = 1, 2, …, K выполнение алгоритма прекращается. В противном случае выполнение переносится к шагу 2.