
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции правдоподобия
|
|
Существует класс областей, где процесс порождения распознаваемых образов находится под влиянием ряда случайных факторов. К таким областям можно в первую очередь отнести задачи интерпретации физических явлений, данные о которых снимаются приборами, подверженными действию шумов и искажений. Например, речь может идти об анализе ЭКГ, аэрофотоснимков, сканированных изображений. В этих случаях важную роль играет аппарат статистического анализа.
В условиях влияния случайных факторов процесс распознавания может представляться как игра распознающего устройства с реальным миром, в которой машина пытается угадать образ, задуманный природой. Этот процесс аналогичен игре двух лиц с нулевой суммой. Это означает, что в каждый момент времени выигрыш одного игрока в точности равен проигрышу второго. В играх такого типа используют различные стратегии поведения, такие как Байесовская стратегия, минимаксная стратегия и стратегия Неймана-Пирсона. Задача классификатора состоит в поиске такой стратегии, которая обеспечивала бы минимальность среднего проигрыша.
Представим игру формально в виде тройки G = (Y, Z, L), где Y и Z — множества произвольной природы, L — ограниченная числовая функция, определённая на множестве прямых произведений (Y × Z). Элементы y ∈ Y и
z ∈ Z представляют стратегии первого и второго игроков соответственно, а функция L интерпретируется как функция выигрыша или функция потерь. На каждом шаге игры первый игрок выбирает элемент своей стратегии y ∈ Y, а второй — элемент z ∈ Z своей. Если побеждает первый игрок, он получает выигрыш, равный значению L (y, z), который выплачивается вторым игроком. Если побеждает второй игрок, то сумму L (y, z) выплачивает ему первый игрок. Игра G называется конечной, если множества Y и Z содержат конечные количества элементов:
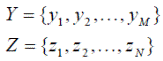
В этом случае функцию L можно задать в виде матрицы размером M × N с элементами Lij = L (yi, zj), которую называют матрицей выигрышей или матрицей потерь. Элемент Lij матрицы потерь определяет проигрыш первого игрока, выбравшего ход yi, при условии, что второй игрок выбрал ход zj. Принято считать положительные значения Lij истинными потерями, а отрицательные — выигрышами.
В контексте задачи распознавания будем считать первым игроком природу, элементами стратегии которой являются классы ω i предъявляемых ею образов x, а вторым игроком — распознаватель, оперирующий решениями относительно возможных принадлежностей объектов x классам ω i. Будем считать, что число элементов в обоих множествах одинаково, хотя в общем случае это может быть и не так.
В каждой игре, т.е. на каждом сеансе распознавания, природа предъявляет объект x, принадлежащий классу ω i в соответствии с априорной вероятностью p (ω i). Эта вероятность просто определяет вероятность встретить произвольный объект класса ω i.
Таким образом, в распоряжении второго игрока оказывается описание объекта x с неизвестной принадлежностью к одному из классов. Его задача как распознавателя заключается в выборе элемента свой стратегии, соответствующего задуманного первым игроком классу. Следует отметить, что игрок-природа не является «разумным противником», который осуществляет свои ходы с целью максимизировать свой выигрыш и принести наибольшие убытки своему сопернику. Можно допустить, что стратегия этого игрока полностью определяется набором априорных вероятностей p (ω 1), p (ω 2), …, p (ω M). Следовательно, это знание может быть использовано игроком-распознавателем при построении своей стратегии.
Итак, игрок-природа предъявляет образ x. Вероятность его принадлежности классу ω i определяется величиной p (ω i | x). Если распознаватель относит объект к классу ω j, а на самом деле он принадлежит классу ω i, то распознаватель терпит убытки в размере Lij. Т.к. объект может принадлежать любому из классов, то математическое ожидание потерь, возможных в результате отнесения его классу ω j, будет равно величине
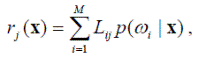 (4.7)
(4.7)
называемой условным средним риском или условными средними потерями.
Если для каждого предъявленного объекта x вычисляются значения условных средних потерь r 1(x), r 2(x), …, rM (x) и классификатор причисляет объект к классу, которому соответствует наименьшая из этих величин, то и математическое ожидание полных потерь на множестве всех решений будет минимизировано. Классификатор, минимизирующий математическое ожидание общих потерь, называется байесовским классификатором. Со статистической точки зрения такой классификатор соответствует оптимальному качеству классификации (распознавания).
Используя формулу Байеса
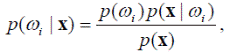
представим (4.7) в следующем виде:
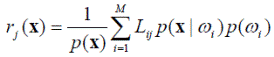
Выражение 1/ p (x) присутствует во всех выражениях ri (x), i = 1, …, M, следовательно его можно исключить:
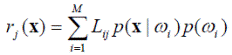 (4.8)
(4.8)
p (x | ω i) называется функцией правдоподобия для класса ω i.
При рассмотрении задачи разделения на два класса, объект x будет отнесён к классу ω 1 при выполнении условия r 1(x) < r 2(x). Раскрывая это условие при помощи (4.8) с подстановкой M = 2, получим следующую его запись:
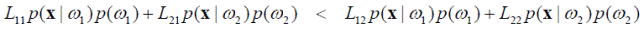
или
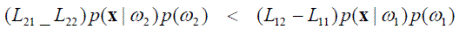
Обычно считается, что Lij > Lii при i ≠ j. При этом допущении получаем
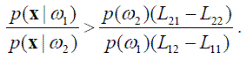 (4.9)
(4.9)
Выполнение этих условий определяет отнесение объекта x к классу ω 1. При этом левую часть неравенства (4.9) называют отношением правдоподобия:
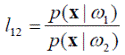
Итак, для случая двух классов, имеем следующее байесовское решающее правило:
• если выполнено l 12(x) > θ 12, то образ x зачисляется в класс ω 1;
1. если выполнено l 12(x) < θ 12, то образ x зачисляется в класс ω 2;
2. если выполнено l 12(x) = θ 12, то решение принимается произвольным образом.
Величину θ 12 называют пороговым значением:
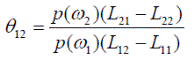
Рассмотрим случай разделения пространства образов на M > 2 классов. В этом случае байесовское правило относит объект x к классу ω i при выполнении условия ri (x) < rj (x), j = 1, 2, …, M; j ≠ i, которое в расширенной форме выглядит как
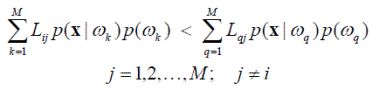
Это неравенство также может быть представлено с использованием отношений правдоподобия и пороговых величин, если принять
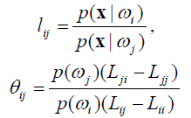
Для лучшего представления общего правила разделения на несколько классов целесообразно воспользоваться функцией потерь специального вида. Во многих задачах распознавания при правильном принятии решения потери считаются нулевыми, а потери при любом неправильном решении считаются одинаковыми и равными, например, 1:
Lij = 0, i = j
Lij = 1, i ≠ j
При использовании такой функции величину средних потерь можно записать как
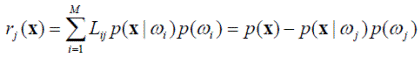
Тогда отнесение объекта x к классу ω i выполняется байесовским правилом при истинности условия
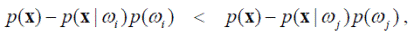
или
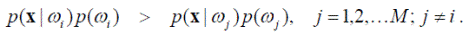
Заметим, что это выражение байесовского решающего правила эквивалентно решающей функции (см. выше) следующего вида
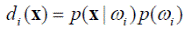 (4.10).
(4.10).
Образ x зачисляется в класс ω i при выполнении условия di (x) > dj (x), ∀ j ≠ i, что соответствует случаю 3 разбиения пространства на несколько классов решающими функциями.
Если преобразовать полученное выражение решающей функции с помощью формулы Байеса, получим формулу
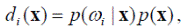
в которой множитель p (x) может быть исключён, что даёт
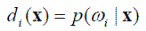 (4.11).
(4.11).
Формула (4.11) по сравнению с (4.10) избавляет решающее правило от необходимости знания в явном виде вероятностей p (x | ω i) и p (ω i). Заметим, что хотя оба выражения эквивалентны, они представляют разные правила классификации.
Поскольку оценка априорной вероятности классов p (ω i), i = 1, …, M обычно не вызывает затруднений, основное различие состоит в том, что в первом случае используются функции правдоподобия p (x | ω i), а во втором — вероятности p (ω i | x) ω принадлежности объекта x к классу ω i.
К классу методов, использующих Евклидово пространство описаний, можно также отнести нейросетевые методы. Нейронные сети способны решать как задачи распознавания, так и автоматической классификации, допуская обучение как с учителем, так и без него.