Изоморфизм графов

Распознавание графов

ЦЕЛЬ РАБОТЫ

5.1.1 Ознакомиться с теоретическими сведениями по теме «Классификация графов».

5.1.2 Получить практические навыки по распознаванию графов.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

5.2.1 Методические указания по выполнению практической работы.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

5.3.1 Изучить методические указания к практической работе.

5.3.2 В соответствии с полученным вариантом распознать следующие графы, определив:

· двудольность;

· изоморфимз;

· связность;

· ориентированность;

· вид:

o полный

o звездный

СОДЕРЖАНИЕ ОТЧЕТА

5.4.1 Цель работы

5.4.2 Методические рекомендации

5.4.3 Порядок выполнения работы

5.4.4 Ответы на контрольные вопросы

5.4.5 Выводы

КОНТРОЛЬНЫЕ ВОПРОСЫ

5.5.1 Что такое граф?

5.5.2 Дайте определение двудольному графу?

5.5.3 Какой граф называется тривиальным?

5.5.4 Дайте определение изоморфизму?

5.5.5 Какой граф называется связным?

5.5.6 Какой граф называется полным?

5.5.7 Дайте определение звездному графу?

5.5.8 Дайте определение Эйлеровому графу?

5.5.9 Дайте определение Полуэйлеровому графу?

5.5.10 Дайте определение Гамильтонову графу?

5.5.11 Дайте определение Полугамильтонову графу?

ПРИЛОЖЕНИЕ 1

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

ИЗОМОРФИЗМ ГРАФОВ

Изоморфизм графов – это отношение эквивалентности. Граф рассматриваются с точностью до изоморфизма, то есть рассматриваются классы эквивалентности по отношению изоморфизма.

Графы называются изоморфными, если существует взаимно-однозначное соответствие между их ребрами и вершинами, причем соответствующие ребра соединяют соответствующие вершины.

Пример

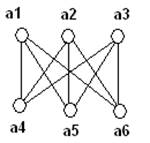
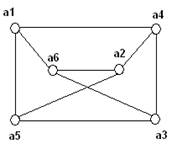
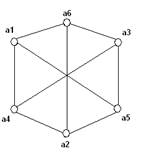
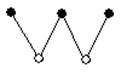
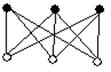
Три внешне различные диаграммы, являются диаграммами одного и того же графа К3, 3. Они изоморфны

Р(а1)=3, Р(а2)=3, Р(а3)=3, Р(а4)=3, Р(а5)=3, Р(а6)=3

Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа.

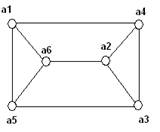
Диаграммы неизоморфных графов с совпадающими инвариантами

Тривиальные и полные графы

Граф, состоящий из одной вершины, называется тривиальным.

Полный граф – это такой граф, между любыми двумя вершинами которого есть ребро.

В полном графе все ребра смежные Кn, где n – это число вершин

Кn=К₄

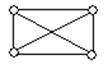
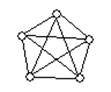
Полный подграф (некоторого графа) называется кликой (этого графа).

Двудольные и звездные графы

Звездный граф – это граф, в котором 1 из вершин является концевой для всех ребер.

К₁, n К₁, ₃

Граф называется двудольным (биграф, четный граф), если его вершины разбиты на два непересекающихся подмножества (можно раскрасить 2мя цветами), а ребра связывают вершины только из разных классов (не обязательно все пары).

Кm, n К_{2, 3}