Связность

Говорят, что две вершины в графе связаны, если существует соединяющая их (простая) цепь. Граф, в котором все вершины связаны, называется связным.

Отношение связанности вершин является эквивалентностью. Классы эквивалентности по отношению связанности называется компонентами связности графа. Число компонент связности графа G обозначается k(G). Граф G является связным тогда и только тогда, когда k(G)=1. если k(G)> 1, то G – несвязный граф. Граф, состоящий только из изолированных вершин, называется вполне несвязным.

Цепь – последовательность идущих друг за другом ребер.

ОПЕРАЦИИ НАД ГРАФАМИ:

1. Дополнение графа

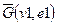
2. Объединение графов

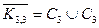
3. Соединение графов – для того, чтобы соединить 2 графа необходимо каждую вершину графа G1 соединить с каждой вершиной графа G2.

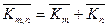
4. Удаление вершины из графа

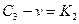
5. Удаление ребра из графа

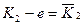
6. Добавление вершины в граф

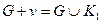
7. Добавление ребра в граф