
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глюкоза фруктоза
|
|
При постоянной температуре скорость данной реакции прямо пропорциональна произведению концентраций реагирующих веществ, причём каждая из концентраций участвует в степени, в простейших случаях равной коэффициенту перед формулой данного вещества в уравнении реакции.
Этим правилом и определяется влияние концентрации на скорость реакции. Оно было выражено (в несколько иной форме) впервые Гульдбергом[2] и Вааге[3] (1867). Его также называют законом действия масс, как и закон, выражающий константу равновесия, ибо оба они тесно связаны между собой. Для газовых реакций это правило является строгим только в пределах применимости законов идеальных газов. Оно применимо также и к реакциям в разбавленных растворах (строго только для бесконечно разбавленных растворов). В математической форме в применении, например, к реакции
2NO + H2 = N2O + H2O
оно выражается в виде
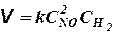
Коэффициент пропорциональности k для каждой данной реакции при постоянной температуре является величиной постоянной и называется константой скорости реакции. Он численно равен скорости реакции в условиях, когда концентрации каждого из исходных веществ равны единице.
Кинетическая классификация химических реакций. В отношении кинетики химические реакции разделяют или по признаку молекулярности реакции, или по признаку порядка реакции. Рассмотрением вопросов, связанных с порядком реакции, мы займёмся позднее. Молекулярность реакции определяется числом молекул, одновременным взаимодействием между которыми осуществляется акт химического превращения. По этому признаку реакции разделяются на одномолекулярные (или мономолекулярные), двухмолекулярные (или бимолекулярные) и трёхмолекулярные (или тримолекулярные).
Можно говорить и о более высокой молекулярности, но в действительности одновременное столкновение трёх молекул уже является очень маловероятным и трёхмолекулярные реакции встречаются крайне редко. Реакций же более высокой молекулярности практически неизвестно. В тех случаях, когда уравнение реакции указывает, что в реакции принимает участие большое число молекул, процесс практически проходит более сложным путём – через две или большее число стадий последовательно протекающих реакций, в каждой из которых взаимодействие осуществляется при столкновении двух или – редко - трёх молекул. Поскольку такие столкновения во много раз более вероятны, то течение реакции по такому (на первый взгляд более сложному) пути совершается с гораздо большей скоростью. Существуют и другие причины усложнения кинетики химических реакций. Однако большей частью любую данную сложную реакцию можно рассматривать как определённую совокупность последовательно или параллельно, или в другой форме сочетающихся простых реакций.
К одномолекулярным реакциям относятся некоторые реакции разложения молекул и внутримолекулярных перегруппировок, например, газовая реакция:
I2 = 2I
Для простых одномолекулярных реакций
V = kC (3)
где С – концентрация исходного вещества.
Или, согласно (2)
 (4)
(4)
где k имеет размерность обратного времени (t-1), выражается в сек-1, мин-1 или в других соответствующих единицах.
К двухмолекулярным реакциям относятся такие, в которых взаимодействие происходит при столкновении двух молекул различного или одинакового вида:
H2 + I2 = 2HI или 2HI = H2 + I2
Примером их может служить также реакция этерификации:
CH3COOH + C2H5OH = CH3COOC2H5 + H2O
Для простых двухмолекулярных реакций
V = kC1C2 (5)
где С1 и С2 – концентрации исходных веществ.
Согласно (2) для этих реакций
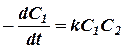 (6)
(6)
В частном случае, когда С1 = С2
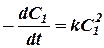 (7)
(7)
Для двухмолекулярных реакций k имеет размерность l3m-1t-1 и выражается обычно в литрах на моль в секунду (или минуту).
Если какое-нибудь из реагирующих веществ содержится в очень большом избытке, то относительное изменение его концентрации в ходе реакции незначительно, т.е. его концентрация изменяется слабо или остаётся практически постоянной.
К трёхмолекулярным реакциям должны быть отнесены реакции, в которых для взаимодействия необходимо одновременное столкновение трёх молекул одного или различных видов. В общем случае уравнение скорости простых трёхмолекулярных реакций имеет вид:
V = kC1C2C3 (8)
Примером трёхмолекулярной реакции может служить указанная выше реакция
2NO +H2 = N2O + H2O
Порядок реакции. Порядок химической реакции определяется по более формальному признаку, чем её молекулярность, - по виду уравнения, выражающего зависимость скорости реакции от концентраций реагирующих веществ. Порядок реакции равен сумме показателей степеней концентрацийв уравнении, выражающем зависимость скорости реакции от концентраций реагирующих веществ. Реакции разделяются на реакции первого порядка, второго порядка, третьего порядка (реакции более высоких порядков не встречаются). Кроме того, известны так называемые реакции нулевого порядка и некоторые реакции, порядок которых выражается дробным числом.
К реакциям первого порядка относят реакции, в которых зависимость скорости от концентрации описывается уравнениями (3) и (4), к реакциям второго порядка – реакции, описываемые уравнениями (5), (6), (7) и т.д.
Прежде такое разделение считали совпадающим с делением, описанным выше, и принимали, что все одномолекулярные реакции являются реакциями первого порядка, и наоборот, а все двухмолекулярные реакции являются реакциями второго порядка, и наоборот. Однако, вследствие различных осложнений, это отнюдь не обязательно.
Скорость химической реакции определяется совокупностью огромного числа элементарных актов взаимодействия между молекулами (или атомами, или ионами). Акты эти могут быть одинаковыми (в простых реакциях) или различными, происходящими параллельно или последовательно[4]. Кроме того, в некоторых случаях один из компонентов реакции присутствует в таком большом избытке, что расход его в реакции практически не отражается на его концентрации. Так, при омылении водой сложного эфира (т.е. при гидролизе его) в разбавленном водном растворе по уравнению вида
СН3СООС2Н5 + Н2О = СН3СООН + С2Н5ОН
концентрация воды изменяется весьма незначительно, и скорость реакции зависит лишь от изменения концентрации эфира. Кинетика этой реакции описывается уравнениями кинетики реакций первого порядка, хотя реакция является по существу бимолекулярной.
 Реакциями нулевого порядка называют процессы, в которых скорость реакции сохраняется постоянной во времени. Это встречается в некоторых гетерогенных системах. Так, если в предыдущем примере – омыление сложного эфира водой в разбавленном водном растворе – применять эфир, малорастворимый в воде, и взять его в избытке, чтобы в системе присутствовал эфирный слой, то расход эфира будет постоянно восполняться из эфирного слоя. Таким образом, концентрация его в водном слое (где протекает реакция) будет постоянной и, следовательно, постоянной будет скорость процесса V = const.
Реакциями нулевого порядка называют процессы, в которых скорость реакции сохраняется постоянной во времени. Это встречается в некоторых гетерогенных системах. Так, если в предыдущем примере – омыление сложного эфира водой в разбавленном водном растворе – применять эфир, малорастворимый в воде, и взять его в избытке, чтобы в системе присутствовал эфирный слой, то расход эфира будет постоянно восполняться из эфирного слоя. Таким образом, концентрация его в водном слое (где протекает реакция) будет постоянной и, следовательно, постоянной будет скорость процесса V = const.
Реакции первого порядка. Разделяя переменные в уравнении (4)
 (9)
(9)
и интегрируя его, получаем:
lnC = - kt + B (10)
Обозначая через С0 начальную концентрацию (при t = 0), определяем постоянную интегрирования B = lnC0. Отсюда
 (11)
(11)
или
 (12)
(12)
Это уравнение выражает зависимость концентрации от времени для реакций первого порядка. Если через х = С0 - С обозначить уменьшение концентрации исходного вещества к моменту времени t, то уравнению этому можно придать вид:
 (13)
(13)
Примером реакции первого порядка, протекающей в растворе, служит реакция гидролитического разложения сахара в разбавленном водном растворе с образованием глюкозы и фруктозы (реакция называется инверсией сахара):
С12Н22О11 + Н2О = С6Н12О6 + С6Н12О6
глюкоза фруктоза
В таблице 1 приведены наблюдённые в опытах по инверсии сахара изменения концентрации во времени и рассчитанные отсюда значения константы скорости.
Кинетика процессов радиоактивного распада описывается также кинетическими уравнениями реакций первого порядка.
Для кинетики реакций первого порядка характерно, что в левой части этих уравнений, например в уравнении (11), содержится только отношение концентраций. При изменении обеих концентраций в одинаковое число раз промежуток времени t не изменяется.
Таблица 1.
Скорость реакции тростникового сахара [1, стр. 469]
| t мин | 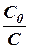
| k | t мин | 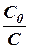
| k |
| - | 14 170 | 2, 117 | 5, 29∙ 10-5 | ||
| 1 435 | 1, 081 | 5, 43∙ 10-5 | 16 935 | 2, 466 | 5, 33∙ 10-5 |
| 4 315 | 1, 266 | 5, 47∙ 10-5 | 19 815 | 2, 857 | 5, 30∙ 10-5 |
| 7 070 | 1, 464 | 5, 39∙ 10-5 | 29 925 | 4, 962 | 5, 35∙ 10-5 |
| 11 360 | 1, 830 | 5, 32∙ 10-5 |
Следовательно, если в одном опыте концентрация через n минут станет вдвое меньше начальной, то и в других опытах (при других начальных концентрациях) в данной реакции она за n минут уменьшится тоже в два раза. Это означает, что за одинаковые промежутки времени прореагирует одинаковая доля взятого количества исходного вещества. Так, если за первые 10 минут в реакцию вступило 5% взятого количества вещества, то за следующие 10 минут прореагируют 5% от оставшихся 95% исходного вещества.
Для характеристики скорости реакций первого порядка (и процессов радиоактивного распада) наряду с константой скорости часто пользуются величиной, называемой периодом полураспада τ, равным промежутку времени, в течение которого реагирует половина взятого количества вещества. Принимая  , находим из уравнения (11)
, находим из уравнения (11)
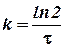 (14)
(14)
Подставляя значение ln 2 = 0, 6932, получаем  . Это соотношение показывает, что константа скорости реакции первого порядка обратно пропорциональна периоду полураспада.
. Это соотношение показывает, что константа скорости реакции первого порядка обратно пропорциональна периоду полураспада.
Благодаря тому, что константы скорости зависят только от отношения концентраций, можно заменять их при расчётах другими пропорциональными величинами. Часто вместо отношения концентраций пользуются отношением количества вещества, а в газовых реакциях – отношением давлений.
Пример. Исследование α -радиоактивного распада изотопа полония с массой 210 показало, что за 14 дней его активность уменьшилась на 6, 85%. Определить константу скорости его распада, период полураспада и рассчитать, в течение какого промежутка времени он разлагается на 90, 0%.
Решение. При разборе радиоактивных процессов в уравнение (11) вместо концентрации подставляют количества вещества. Принимая начальное количество за 100%, определяем по условию, что после 14 дней осталось неразложенным 93, 15%, откуда константа скорости согласно (11) определяется из равенства

или

Отсюда
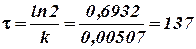 дней
дней
Промежуток времени tx, за который продукт разложится на 90, 0%, т.е. останется неразложенным 10, 0%, определяется из равенства

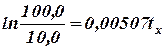
откуда
 дня
дня
Реакции второго порядка. Вывод уравнения кинетики реакций второго порядка рассмотрим только для простейшего случая, когда концентрации двух реагирующих веществ являются одинаковыми. Пользуясь уравнением (5) при условии, что С0, 1 = С0, 2 = С и 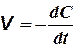 , и разделяя переменные, получаем:
, и разделяя переменные, получаем:
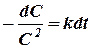 (15)
(15)
откуда после интегрирования
 (16)
(16)
где постоянная интегрирования В может быть определена, если известна концентрация С для какого-нибудь данного момента времени t. Так, если известна начальная концентрация С0 при t =0, то
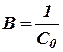
Отсюда

или
 (17)
(17)
Если вместо концентрации С ввести убыль концентрации реагирующего вещества х = С0 - С, то уравнение (17) легко приводится к виду:
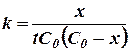 (18)
(18)
Если начальные концентрации С0, 1 и С0, 2 исходных веществ неодинаковы, то конечное уравнение, отвечающее уравнению (18), будет иметь вид:
 (19)
(19)
Это уравнение можно вывести, исходя из общего выражения скорости двухмолекулярной реакции

Уравнения (18) и (19) хорошо подтверждаются опытными данными.
Если отнести уравнение (18) к моменту времени τ, когда израсходована половина взятого количества рассматриваемого исходного вещества, т.е. принять 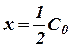 , то уравнение (18) будет иметь вид:
, то уравнение (18) будет иметь вид:
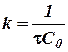 или
или 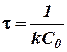 (20)
(20)
Сравнивая его с уравнением (14), легко видеть, что в отличие от реакций первого порядка в реакциях второго порядка промежуток времени, в течение которого прореагирует половина взятого количества, зависит от начальной концентрации реагирующих веществ. Это означает, что период полураспада в реакциях второго порядка (а также и более высоких порядков) зависит от концентрации реагирующих веществ.
Сложные реакции. Кинетика сложных реакций, состоящих из двух или большего числа простых реакций, в той или иной форме связанных между собой, зависит от формы связи между этими реакциями и от соотношения их скоростей. Типичными по форме такой связи являются реакции параллельные, последовательные (консекутивные), сопряжённые и обратимые. Теория этих реакций основывается на положении, что при протекании в системе одновременно нескольких реакций каждая из них происходит самостоятельно и к каждой из них в отдельности применимы уравнения кинетики простых реакций.
Параллельными называются реакции вида

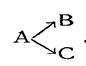
При таких реакциях данное исходное вещество или исходные вещества могут реагировать одновременно в различных направлениях. Примером параллельных реакций является реакция разложения хлората калия, которая при умеренных температурах может совершаться параллельно в двух направлениях

Некоторые радиоактивные элементы распадаются параллельно по двум направлениям. Наиболее часто параллельные реакции встречаются в органической химии. Так, например, при нитровании фенола азотной кислотой нитрогруппа может занимать или орто- или пара-положение.
Если в данных условиях термодинамически возможны два или три направления химической реакции, то преобладание того или другого из них и относительные количества получаемых продуктов реакции определяются всецело соотношением скоростей этих реакций, а не соотношением термодинамической устойчивости конечных продуктов.
Если реакции значительно различаются по скорости, то обычно реакцию, обладающую большей скоростью, называют главной (основной), а остальные побочными. Впрочем, при не слишком большом различии в скоростях главной реакцией называют реакцию, приводящую к получению основного нужного продукта, хотя бы она и обладала меньшей скоростью.
Последовательными (консекутивными) называются реакции вида
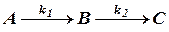 (а)
(а)
где вещество В является промежуточным продуктом в процессе получения вещества С, а k1 и k2 - константы скоростей двух стадий превращения.
Схема (а) представляет простейшую последовательную реакцию; протекает она в две ступени, и каждая из них является простой мономолекулярной реакцией. В общем же случае число ступеней в последовательных реакциях может быть и больше двух, и каждая из ступеней может быть не мономолекулярной, а более сложной.
Последовательные реакции широко распространены. К ним относятся, в частности, реакции гидролиза сложных эфиров дикарбоновых кислот, или сложных эфиров гликолей, или дигалоидопроизводных. Кинетику последовательно протекающих процессов радиоактивных превращений можно рассматривать как частный случай кинетики ряда последовательных реакций первого порядка.
Простым примером последовательных реакций может служить омыление диэтилоксалата едким натром, которое протекает последовательно в две стадии:
СООС2Н5 COOC2H5
| + NaOH → | + C2H5OH
COOC2H5 COONa
СООС2Н5 COONa
| + NaOH → | + C2H5OH
COONa COONa
Расчёт кинетики последовательных реакций в общем виде очень сложен. Отметим только, что если одна из ступеней обладает значительно меньшей скоростью, чем остальные, то общая скорость реакции 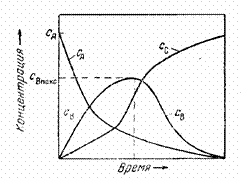 определяется скоростью именно этой ступени.
определяется скоростью именно этой ступени.
На рис. 3 представлен «график Раковского[5]» для простейшей последовательной реакции. График этот выражает зависимость концентраций каждого из веществ от времени. Кривая С А выражает уменьшение концентрации исходного
Рис.3. Зависимость концентра- вещества А. Кривая С С выражает нарастание
ции веществ от времени концентрации вещества С. Кривая
(в последовательной ре- С В показывает изменение во времени
акции) [1, стр. 473] концентрации промежуточного вещества В. В
начале процесса, когда концентрация вещества А ещё сравнительно высока, скорость первой реакции значительна и увеличение концентрации вещества В происходит быстро. По мере израсходования вещества А уменьшается и скорость образования вещества В. Это приводит к тому, что расход вещества В на образование вещества С, начиная с какого-то момента времени, уже не компенсируется в полной степени образованием его из вещества А и концентрация вещества В в системе начинает уменьшаться. Вследствие этого кривая С В проходит через максимум. Положение таких кривых для различных последовательных реакций неодинаково, так как оно зависит от соотношения в скоростях этих реакций. Но общий характер зависимости остаётся обычно таким, как показано на рис. 3.
Сопряжёнными называются реакции вида
A + B → M (б)
A + C → N (в)
из которых одна, например (б), протекает лишь совместно с другой, т.е. она индуцируется последней. В таких случаях вещество С служит индуктором первой реакции. Примером таких реакций может служить окисление сульфата железа (II) и йодистого водорода перекисью водорода. Сульфат железа окисляется независимо от присутствия йодистого водорода, последний же в чистом виде перекисью водорода не окисляется, но при одновременном окислении сульфата железа окисляется совместно с ним. Подобно этому, раствор индиго[6] сам по себе действием кислорода не обесцвечивается, но если к раствору прибавить бензальдегид, то последний окисляется кислородом в бензойную кислоту и одновременно индиго окисляется в изатин и раствор обесцвечивается.
Это явление, называемое химической индукцией, было детально изучено Н.А. Шиловым[7] (1905). Вещество А, общее для обеих реакций (в наших примерах перекись водорода и кислород), получило название актора, вещество В - акцептора, а вещество С, как было указано выше, - индуктора.
Обратимые реакции. Скорость обратимой реакции равна разности между скоростями прямой и обратной реакций. Если обратиться к общему случаю реакции вида
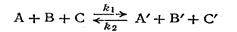
то скорость изменения (убывания) концентрации вещества А при протекании прямой реакции определяется уравнением
 (21)
(21)
а скорость изменения (возрастания) её при протекании обратной реакции - уравнением
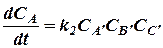 (22)
(22)
Если в начальном состоянии системы в ней содержались только вещества А, В, С, то скорость прямой реакции уменьшается по мере течения её в соответствии с уменьшением этих концентраций. Таким образом, зависимость  этой скорости от времени представляется кривой I на
этой скорости от времени представляется кривой I на  рис. 4; если бы не было обратной реакции, эта кривая достигла бы оси абсцисс при израсходовании одного из исходных веществ.
рис. 4; если бы не было обратной реакции, эта кривая достигла бы оси абсцисс при израсходовании одного из исходных веществ.
Кривая II, относящаяся к скорости обратной реакции, начинается в начале координат (так как по условию в начальный момент А' = В' = С' = 0) и повышается по мере течения прямой реакции и Рис. 4. Зависимость ско- вызываемого ею увеличения этих концентраций. Общая
ростей прямой и обрат- скорость реакции в любой данный момент равна
ной реакций от времени разности скоростей прямой и обратной реакций