
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
в обратимой реакции
|
|
[1, стр. 475]  (23)
(23)
Очевидно, при дальнейшем течении реакции указанные две кривые – скоростей прямой и обратной реакций – должны где-то пересечься, т.е. должно быть достигнуто такое состояние, при котором скорости V1 прямой и V2 обратной реакций станут равными. Легко убедиться, что после достижения этого концентрации каждого из компонентов реакции будут постоянными. Таким образом, в системе будет достигнуто состояние равновесия, когда скорости прямой и обратной реакций будут равны между собой по абсолютной величине. Следовательно, должны быть равны между собой и правые части уравнений (21) и (22)
 (24)
(24)
откуда
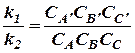 (25)
(25)
Правая часть этого равенства представляет собой константу равновесия К данной реакции, и, следовательно
 (26)
(26)
т.е. константа равновесия равна отношению констант скоростей прямой
и обратной реакций.
Этот вывод чётко показывает динамический характер равновесия в химических реакциях.
Влияние изменения внешних условий на равновесие. Влияние изменения температуры на термодинамические равновесия в общем виде было впервые установлено А.Л. Потылицыным[8] (1880). Через несколько лет это влияние было выражено Вант-Гоффом[9] (1883) в количественной форме. Немного позже Ле Шателье[10] (1885), а затем Браун (1886) сформулировали общий принцип, отражающий влияние изменения различных факторов на положение равновесия, - принцип смещения равновесий, называемый иначе принципом Ле Шателье, который можно выразить следующим образом.
Если на систему, находящуюся в устойчивом равновесии, воздействовать извне, изменяя какое-нибудь из условий, определяющих положение равновесия, то в системе усилится то из направлений процесса, течение которого ослабляет влияние произведенного воздействия, и положение равновесия сместится в том же направлении.
Учитывая, что истинное равновесие всегда отвечает равенству скоростей прямого и обратного процессов, можно сказать, что смещение равновесия происходит в том случае, когда произведенное воздействие неодинаково влияет на скорости прямого и обратного процессов. Это нарушение равенства скоростей и приводит к смещению равновесия и переходу системы в новое состояние равновесия, при котором скорости прямой и обратной реакций опять станут одинаковыми между собой, но будут отличаться от первоначальных.
Рассмотрим влияние изменения только двух важнейших факторов, определяющих положение равновесия, - температуры и давления.
Возьмем для примера систему, состоящую из азота, водорода и аммиака, находящихся в химическом равновесии:

 Рассмотрим сначала влияние изменения температуры. Как будет смещаться равновесие в этой системе при повышении температуры? Реакция образования аммиака сопровождается выделением теплоты (экзотермическая реакция). При обратной же реакции теплота, очевидно, поглощается (эндотермическая реакция). Повысить температуру системы, находящейся в равновесии, можно только,
Рассмотрим сначала влияние изменения температуры. Как будет смещаться равновесие в этой системе при повышении температуры? Реакция образования аммиака сопровождается выделением теплоты (экзотермическая реакция). При обратной же реакции теплота, очевидно, поглощается (эндотермическая реакция). Повысить температуру системы, находящейся в равновесии, можно только,
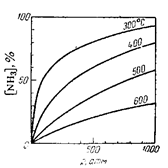
Рис. 5. Влияние тем- подводя к ней теплоту извне. Такое воздействие вызовет
пературы и давления усиление того из направлений реакции, которое
на положение равно- сопровождается поглощением теплоты, т.е.
весия в реакции син- диссоциацию аммиака (рис. 5). Это смещение равновесия
теза аммиака. По оси ослабит влияние оказанного внешнего воздействия. В
ординат отложено самом деле, зная теплоёмкости азота,
содержание аммиака водорода и аммиака, мы могли бы для какого-нибудь
в равновесной смеси данного количества их смеси известного состава,
с азотом и водородом находящейся в равновесии, рассчитать, какое
(при отношении N2: H2= количество теплоты нужно подвести к этой системе для
=1: 3) [1, стр. 237] повышения температуры её, например, на 100°С. Однако
химическая реакция (в данном случае диссоциация аммиака) поглотит часть введенной теплоты и в результате то же количество теплоты вызовет повышение температуры не на 100°С, а соответственно в меньшей степени.
Указанное явление происходит потому, что с повышением температуры неодинаково увеличиваются скорости прямого и обратного процессов. Скорость эндотермической реакции возрастает сильнее. Это и вызывает смещение равновесия до состояния, при котором скорости прямой и обратной реакций станут опять равными между собой. С понижением температуры равновесие будет смещаться в сторону образования аммиака.
В общей форме влияние изменения температуры можно выразить таким образом:
Повышение температуры всегда благоприятствует накоплению тех веществ, которые образуются в данной реакции с поглощением теплоты, т.е. усиливает эндотермическое направление процесса. Понижение температуры действует в противоположном направлении.
Чем бó льшим тепловым эффектом обладает данный процесс, тем сильнее смещается равновесие с изменением температуры. В процессах же, в которых тепловой эффект мал, равновесие при изменении температуры смещается незначительно.
Рассмотрим влияние изменения давления для той же реакции, выяснив, как будет смещаться равновесие при повышении давления. Повышение давления усилит то из направлений процесса, которое сопровождается уменьшением объёма, и это ослабит влияние произведенного воздействия.
Для газовых реакций изменение объёма приближённо можно определить, считая, что объёмы одного моля различных газов при одинаковых температуре и давлении одинаковы. В нашей реакции из одного моля азота и трёх молей водорода получается два моля аммиака, т.е. течение реакции в прямом направлении сопровождается уменьшением объёма в два раза (из четырёх объёмов получается два). Следовательно, обратная реакция сопровождается таким же увеличением объёма. Повышение давления при постоянной температуре и постоянных количествах реагирующих веществ можно осуществить, только сжимая систему, т.е. уменьшая её объём. Такое воздействие вызовет усиление в системе того процесса, который сопровождается уменьшением объёма, т.е. в данном случае образование аммиака. Понижение давления должно, наоборот, способствовать образованию аммиака (см. рис. 5).
Это смещение равновесия и ослабит влияние произведенного воздействия. В самом деле, если газовая смесь находится в условиях, когда к ней применимы законы идеальных газов, то при отсутствии смещения химического равновесия для повышения давления в два раза требовалось бы уменьшить объём тоже в два раза. Однако при образовании аммиака общее число молей газа сокращается, и поэтому уменьшение объёма в два раза приводит к повышению давления не в два раза, а в меньшей степени.
В реакциях, происходящих с участием газообразных веществ, с повышением давления равновесие смещается в сторону веществ, содержащих меньшее число молей газов. В общей же форме влияние изменения давления на положение равновесия можно выразить следующим образом:
Повышение давления благоприятствует образованию веществ, занимающих в данных условиях меньший объём, т.е. усиливает то из направлений процесса, которое сопровождается уменьшением объёма. Понижение давления действует в противоположном направлении.
Чувствительность положения равновесия к изменениям давления оказывается тем большей, чем бó льшим изменением объёма сопровождается данный процесс. В процессах же, в которых изменение объёма незначительно, равновесие слабо смещается при изменении давления.
Значительные изменения объёма могут происходить только в реакциях, в которых участвуют газы, т.е. когда хотя бы один из компонентов находится в газообразном состоянии. В процессах же, происходящих в конденсированных фазах, ни один из компонентов реакции не находится в газообразном состоянии и, следовательно, значительных изменений объёма происходить не может. Поэтому в таких процессах изменением давления не удаётся достичь значительных смещений равновесия, как это часто удаётся в реакциях с участием газообразных продуктов.
Принцип смещения равновесий распространяется и на другие факторы. Если равновесие в процессе зависит от внешних электрических, магнитных полей или поля тяготения, то при изменении их усиливается то из направлений процесса, которое уменьшает влияние произведенного воздействия. Точно так же влияет и введение дополнительных количеств одного из компонентов реакции, в чём можно убедиться из рассмотрения константы равновесия.
Химическая термодинамика даёт метод количественного выражения всех этих влияний.

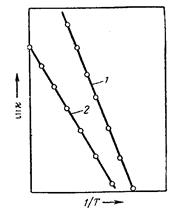
 Влияние температуры на скорость реакций. Энергия активации. При повышении температуры скорость химических реакций увеличивается; это увеличение весьма значительно. Так, скорость реакции 2Н2 + О2 = 2Н2О при 300°С неизмеримо мала, а при 700°С реакция протекает уже мгновенно, в форме взрыва. Общий характер зависимости скорости реакции от температуры иллюстрируется кривыми рис. 6.
Влияние температуры на скорость реакций. Энергия активации. При повышении температуры скорость химических реакций увеличивается; это увеличение весьма значительно. Так, скорость реакции 2Н2 + О2 = 2Н2О при 300°С неизмеримо мала, а при 700°С реакция протекает уже мгновенно, в форме взрыва. Общий характер зависимости скорости реакции от температуры иллюстрируется кривыми рис. 6.
Соотношения, выражающие влияние температуры на скорость реакции, значительно
Рис. 6. Зависимость упрощаются, если рассматривать зависимость
скорости реакции от логарифма константы скорости от обратного
температуры. значения абсолютной температуры. Опытные данные
[1, стр. 476] показывают, что в диаграмме, выражающей связь между
 этими величинами (рис. 7), экспериментальные точки, относящиеся к одной реакции, располагаются обычно практически на одной прямой, т.е. что логарифм константы скорости реакции (ln k или lg k) находится практически в линейной зависимости от обратной температуры (1/Т). Следовательно, искомая зависимость может быть приближённо выражена уравнением вида
этими величинами (рис. 7), экспериментальные точки, относящиеся к одной реакции, располагаются обычно практически на одной прямой, т.е. что логарифм константы скорости реакции (ln k или lg k) находится практически в линейной зависимости от обратной температуры (1/Т). Следовательно, искомая зависимость может быть приближённо выражена уравнением вида
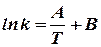 (27)
(27)
где А и В - индивидуальные постоянные, характерные
Рис. 7. Зависимость для данной реакции.
логарифма констан- Это уравнение называется уравнением
ты скорости реакции Аррениуса [11], который нашёл (1889) эту линейную
от обратной темпера- зависимость и предложил следующее объяснение
туры [1, стр. 476] [12] физического смысла постоянной А.
Уравнение изохоры реакции
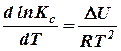 (28)
(28)
выражает изменение константы равновесия с температурой через тепловой эффект реакции.
Подставляя в это уравнение вместо Кс отношение констант скоростей прямой и обратной реакций  (см. уравнение 26), можно получить:
(см. уравнение 26), можно получить:

 (29)
(29)
Рассматривая тепловой эффект реакции как разность двух энергетических величин 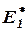 и
и  , относящихся соответственно к прямой и обратной реакциям
, относящихся соответственно к прямой и обратной реакциям 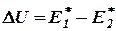 , можно разложить уравнение (29) на два уравнения:
, можно разложить уравнение (29) на два уравнения:
 и
и  (30)
(30)
относящиеся к прямой и обратной реакциям и содержащие одинаковый член С.
Аррениус, считая Δ U постоянным и основываясь на уравнении (27), принял, что 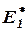 и
и  не зависят от температуры и что С = 0, откуда
не зависят от температуры и что С = 0, откуда
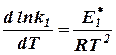 и
и 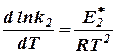 (31)
(31)
Интегрируя эти уравнения, при постоянстве 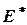 , получаем:
, получаем:
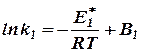 и
и  , (32)
, (32)
где В1 и В2 – постоянные интегрирования.
Величины 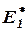 и
и  получили название энергии активации. Они связаны с постоянной А уравнения (27) простым соотношением
получили название энергии активации. Они связаны с постоянной А уравнения (27) простым соотношением  . Как показывают уравнения (30), константа скорости реакции (а следовательно, и скорость реакции) сильнее изменяются с температурой в тех реакциях, в которых энергия активации больше. И наоборот: если в данной реакции энергия активации незначительна, то скорость этой реакции слабо изменяется с температурой.
. Как показывают уравнения (30), константа скорости реакции (а следовательно, и скорость реакции) сильнее изменяются с температурой в тех реакциях, в которых энергия активации больше. И наоборот: если в данной реакции энергия активации незначительна, то скорость этой реакции слабо изменяется с температурой.
Рассмотрим теперь физический смысл энергии активации.
Как было сказано раньше, в реакциях, протекающих с конечной скоростью, число столкновений между молекулами, приводящих к химическому взаимодействию (число эффективных столкновений), составляет лишь некоторую часть общего числа столкновений (большей частью лишь малую долю их). Можно показать, что эффективными оказываются лишь столкновения между такими молекулами, которые в момент столкновения обладают некоторым избытком внутренней энергии по сравнению со средней (для данной температуры) величиной. Именно этот избыток энергии, необходимый молекулам для данной реакции в рассматриваемых условиях её проведения, и представляется энергиями активации 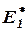 и
и  .
.
Рис. 8 поясняет эти представления. На нём по вертикальной оси отложена энергия рассматриваемой системы молекул, а по горизонтальной – ход реакции. Если прямая реакция (переход из состояния I в состояние II) является экзотермической, то общий запас энергии продуктов реакции меньше, чем исходных веществ, т.е. система в результате этой реакции переходит на более низкий энергетический уровень (с уровня I на уровень II)[13]. Разность уровней I и II равна тепловому эффекту реакции. Уровень К определяет тот наименьший запас энергии, которым должны обладать молекулы, чтобы их столкновения могли приводить к химическому взаимодействию. Разность между этим уровнем К и уровнем I представляет энергию активации прямой реакции, а разность между уровнями Рис. 8. Изменение энергии К и II - энергию активации обратной реакции реакционной системы. Таким образом, по пути из исходного [1, стр. 478]состояния в конечное система должна перейти через своего рода энергетический барьер.
Только активные молекулы, т.е. молекулы, обладающие в момент столкновения необходимым избытком энергии (в нужной форме), могут вступать в соответствующее химическое взаимодействие.
«Активные молекулы» первоначально рассматривали как особую, как бы таутомерную форму молекул реагирующего вещества. Только значительно позднее представление об активных молекулах стало принимать современный вид. Д.В. Алексеев применил (1915-1924) для объяснения природы активных молекул закон распределения молекул по скоростям, показав статистический характер зависимости.
Какие же формы внутренней энергии молекул сказываются на их активности? Во-первых, надо подчеркнуть, что никакой особой формы энергии, отвечающей энергии активации, в молекулах нет. Энергия активации – это то избыточное количество энергии (по сравнению со средней величиной), которой должна обладать молекула в момент столкновения, чтобы быть способной к химическому взаимодействию. Избыточная энергия может быть в молекуле в различных формах; это может быть:
1. повышенная кинетическая энергия поступательного или вращательного движения;
2. повышенная энергия взаимного колебания атомов или атомных групп, составляющих молекулу;
3. повышенная энергия движения тех или иных электронов.
Для различных реакций не все формы этой энергии равноценны[14]. Так, для термической диссоциации йода на атомы I2 = I + I большое значение имеет энергия колебания атомов в молекуле.
Повышенная энергия движения электронов может достигаться при поглощении видимого света (или других электромагнитных колебаний) и переходе электронов на более высокий энергетический уровень (как, например, при активации хлора в реакции H2 + Cl2 = 2HCl). Энергия электронов в атомах может повышаться при разрыве валентной связи, например при диссоциации молекулы водорода на атомы или при образовании других атомов с ненасыщенной валентностью или свободных радикалов. Такая активация может осуществляться и при химических взаимодействиях (как, например, в реакции Na + Cl2 = NaCl + Cl) и при ударах молекул о стенку сосуда и пр. Наконец, молекулы могут активироваться действием электрического разряда, ультразвуковыми колебаниями, действием излучений различного рода и другими путями.
В табл. 2 приведены энергии активации некоторых реакций.
Таблица 2.
Энергия активации Е* (ккал/моль) некоторых реакций  [1, стр. 479]
[1, стр. 479]
| Реакция | Область температур °С | 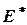
|
| 2Cl2O = 2Cl2 + O2 | 21, 0 | |
| 2NO2 = 2NO + O2 | 32, 0 | |
| H2 + I2 = 2HI | 300÷ 500 | 39, 7 |
| C2H4 + H2 = C2H6 | 43, 5 | |
| 2HI = H2 + I2 | 300÷ 500 | 44, 4 |
| C2H4 = C2H2 + H2 | 780÷ 880 | 60, 00 |
Ранее было отмечено, что системы могут длительное время сохраняться в термодинамически менее устойчивом состоянии, если существуют кинетические препятствия для перехода в более устойчивое состояние. Большая энергия активации и является одним из факторов, определяющих устойчивость систем в кинетическом отношении. Например, смесь Н2 и О2 может длительно сохраняться при комнатной температуре, так как энергия активации реакции взаимодействия между ними весьма значительна[15].
Расчёты констант скоростей и энергии активации. Рассмотрим, как уравнение (27) применяется для выражения зависимости константы скорости от температуры и для определения энергии активации, а также для расчёта константы скорости при различных температурах. Две постоянные в уравнении (27) могут быть определены, если известны значения константы скорости данной реакции 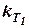 и
и  при двух температурах Т1 и Т2. Имея систему из двух уравнений
при двух температурах Т1 и Т2. Имея систему из двух уравнений

 (33)
(33)
с двумя неизвестными  А и В, мы, вычитая первое уравнение из второго, получим:
А и В, мы, вычитая первое уравнение из второго, получим:
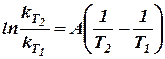 (34)
(34)
Это даёт возможность непосредственно определить А (а следовательно и энергию активации  ). Подставляя полученное значение А в одно из уравнений (33), рассчитывают постоянную В.
). Подставляя полученное значение А в одно из уравнений (33), рассчитывают постоянную В.
Полученное уравнение с численными значениями постоянных А и В можно применять для расчёта константы скорости при промежуточных температурах (т.е. для интерполяции) и в некоторых пределах для экстраполяции.
Пример. Для реакции разложения СО(СН2СООН)2 в водном растворе константа скорости (сек.-1) при 10°С k10 = 1, 080∙ 10-4; при 60°С k60 = 5, 484∙ 10-2. Определить энергию активации и константу скорости реакции разложения СО(СН2СООН)2 при 30°С.
Решение. Уравнение (34) для заданных условий имеет вид:

Переходим к десятичным логарифмам
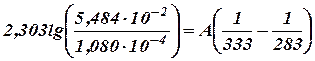


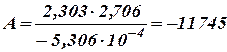

Уравнение (27) (или одно из уравнений (33)) для Т = 283°К и k = 1, 080∙ 10-4 при переходе к десятичным логарифмам и при подстановке найденного значения А принимает вид:
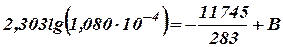
откуда


В результате можно написать уравнение, выражающее для данной реакции зависимость константы скорости от температуры (подставив найденные величины А и В в уравнение (27)):

Константу скорости при 30°С легко получить, подставляя в него Т = 303:
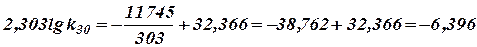

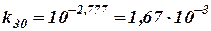
Полученное значение k30 совпадает с найденным измерением при этой температуре k30 = 1, 63∙ 10-3.
Рассмотрим другой способ расчёта.
Обозначим через kt константу скорости данной реакции при t° C и через kt+10 константу скорости той же реакции при температуре (t + 10)°С. Отношение 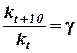 называется температурным коэффициентом скорости.
называется температурным коэффициентом скорости.
При γ < 5 для небольших интервалов температуры можно рассматривать γ как постоянную и выражать приближённо константу скорости kt+n∙ 10 при какой-нибудь температуре (t + n∙ 10°) через kt и γ соотношением[16]:
 (35)
(35)
Здесь n может быть как целым, так и дробным числом, т.е. интервал между этими температурами не обязательно должен быть кратным десяти.
Пользуясь этим соотношением и зная константы скорости данной реакции при двух температурах, можно приближённо определить константы скорости для других (лучше – промежуточных) температур.
Пример. Пользуясь условиями, описанными в примере на стр. 23, определить температурный коэффициент скорости реакции γ и константу скорости k при 30°С.
Решение. Воспользуемся соотношением (35). Логарифмируя его при заданных условиях (n = 5, т.к. разница температур составляет 60 - 10 = 50°), имеем:
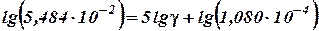
откуда
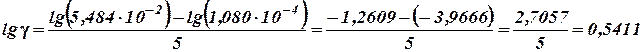
и
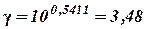
Определяем k30 через k10 и найденное значение γ. В этом случае n = 2 (разница температур 20°). Следовательно:

откуда
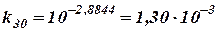
Это значение ~ на 20% отличается от полученного более точным методом.
В приведенной форме этот метод расчёта не имеет преимущества перед методом, основанном на уравнении Аррениуса. При тех же требованиях к исходным данным он достаточно точен лишь в случае применения к небольшим температурным интервалам.
Так, для обычных температур ещё давно было предложено приближённое правило, согласно которому с повышением температуры на 10° скорость реакций увеличивается примерно в 2÷ 4 раза (правило Вант-Гоффа), т.е. γ можно принять равным примерно 2÷ 4. Правило это определяет только порядок изменения скорости, присущего значительной части различных химических реакций при обычных температурах. Однако для ориентировочной оценки возможного влияния температуры это правило нередко бывает полезным, в особенности при отсутствии данных для более точного расчёта.


ЛИТЕРАТУРА
1. Киреев В.А.; Краткий курс физической химии; изд. 4-е, доп. и перераб.;
Химия, М., 1969; 640 стр.
2. Волков В.А., Вонский Е.В., Кузнецова Г.И.; Выдающиеся химики мира.
Биографический справочник; Высшая школа, М., 1991; 656 стр.
3. Гончаров А.И., Корнилов М.Ю.; Справочник по химии; Вища школа, Киев,
1977; 304 стр.
[1] Не во всех случаях нужно увеличивать скорость реакций; иногда требуется её уменьшить [1, стр. 462].
[2] Гульдберг Като Максимилиан (11.VIII.1836-14.I.1902). Норвежский физикохимик и математик, член Норвежской АН (с 1867). Окончил университет в Кристиании (1859). До 1860 преподавал математику в средней школе, в 1861 в Королевской военной школе, с 1861 в Королевской военной академии, с 1867 в университете Кристиании (с 1869 профессор математики).
Основные работы – в области химической кинетики и термодинамики. Установил (1860) зависимость температур плавления сплавов, смесей жирных кислот и смесей солей, а также плотности смесей от состава. Совместно с П. Вааге открыл (1864-1867) закон действующих масс и исследовал условия равновесия. Развил (1870-1872) представления о сущности неопределённых химических соединений, впервые сформулировал (1870) принцип подвижного равновесия. Также совместно с Вааге разработал (1879) молекулярно-кинетическую интерпретацию закона действующих масс и его применения в практике осуществления химических реакций. Ввёл в практику описания фазовых равновесий уравнения состояния и уравнения, связывающие внутреннюю энергию тела с параметрами состояния – давлением и температурой. Ввёл в физику и химию понятие идеального твёрдого вещества, аналогичное понятию идеального газа. Разработал методы сравнительного расчёта свойств веществ, нашёл уравнения для вычисления коэффициентов расширения тел, теплот плавления и теплоёмкостей (1875-1880). Вывел формулы для калориметрических характеристик пара в различных условиях и уравнения зависимости упругости насыщенного пара от температуры. Занимался также метрологией. Автор учебников по теоретической и прикладной математике [2, стр. 138].
[3] Вааге Петер (29.VI.1833-13.I.1900). Норвежский физикохимик и минералог, член Норвежской АН (с 1863). Родился в Флеккефьорде. Получил образование в области медицины и минералогии в университете в Кристиании (1854-1858), затем учился химии во Франции и Германии. С 1861 работал в университете в Кристиании (с 1862 профессор).
Основные научные работы относятся к химической кинетике и термодинамике. Исследования проводил совместно с К.М. Гульдбергом [2, стр. 84].
[4] Уравнение химической реакции отражает в этом случае обычно лишь суммарный эффект этих взаимодействий [1, стр. 467].
[5] Раковский Адам Владиславович (24.CII.1879-7.VI.1941). Советский физикохимик, член-корреспондент АН СССР (с 1933). Родился в Межиречье (Польша). Окончил Московский университет (1903). С 1903 работал в Центральной химической лаборатории министерства финансов, в 1919-1941 - в институте чистых химических реактивов. С 1915 одновременно преподавал в Московском университете (с 1920 профессор).
Основные работы относятся к химической термодинамике. Изучал растворимость солей и равновесия в их водных растворах. Определил упругость паров хлоридов металлов с целью разработки нового металлургического процесса разделения полиметаллических руд и их концентратов путём хлорирования. Исследовал гетерогенные равновесия при высоких температурах. Многие его работы посвящены решению практических задач химической промышленности, в частности вопросам очистки этилового спирта, производства реактивов. Автор учебников для высших учебных заведений: «Курс общей и неорганической химии» (1933), «Введение в физическую химию» (1938), «Курс физической химии» (1939) [2, стр. 367].
[6] Индú го (исп. indigo - название красителя) C16H10N2O2 - кристаллы синего цвета, т.пл. 390°С; трудно растворяется в большинстве органических растворителей, используется в качестве красителя. Раньше индиго добывался из индигоносных растений. Развитие производства синтетического индиго оказало влияние на всю химическую промышленность. В настоящее время культивирование индигоносных растений и получение
из них индиго утратило своё исключительное значение. Индиго – дешёвый кубовый краситель для хлопка и шерсти. Сульфированием индиго получают индигокармин [3, стр. 107].
[7] Шилов Николай Александрович (10.VII.1872-17.VIII.1930). Советский физикохимик. Родился в Москве. Окончил Московский университет (1895). В 1896-1897 совершенствовал образование в Лейпцигском университете. В 1899-1910 работал в Московском университете, с 1910 профессор Московского технического училища, одновременно с 1911 - Московского коммерческого института (впоследствии Институт народного хозяйства).
Работы посвящены кинетике сопряжённых реакций, изучению взаимодействия веществ, находящихся в реакционной системе. Ввёл представления об индукторах и акцепторах; разработал (1905) теорию сопряжённых реакций. Изучал (1909-1910) влияние среды на скорость окислительных реакций. Во время первой мировой войны исследовал адсорбцию отравляющих веществ углём и защитное действие угольного противогаза. Выполнил (1919-1930) обширную серию исследований адсорбции и смежных с нею явлений в коллоидных системах, а также явлений распределения вещества между двумя растворителями и предложил свою формулу распределения. Создал (1929) препарат гиперсол для лечения гипертонии и атеросклероза и объяснил механизм его действия [2, стр. 504].
[8] Потылицын Алексей Лаврентьевич (28.III.1845-10.III.1905). Русский химик. Ученик Д.И. Менделеева. Родился в Красноярске. Окончил Петербургский университет (1872). В 1873-1883 работал там же (с 1881 профессор), в 1883-1895 профессор Варшавского университета, с 1895 директор Новоалександрийского института сельского хозяйства и лесоводства.
Основные работы посвящены физической химии. Доказал (1881), что «правило наибольшей работы» (принцип Бертло-Томсена) безусловно верно только при абсолютном нуле. Установил (1886) зависимость скорости образования солей при двойном обменном разложении от теплот их образования. Развил теорию пересыщения растворов, установив зависимость между способностью вещества легко образовывать пересыщенные растворы и его способностью гидратироваться. Предложил теорию процесса схватывания гипса [2, стр. 356÷ 357].
[9] Вант Гофф Якоб Хендрик (30.VIII.1852-1.III.1911). Голландский химик. Родился в Роттердаме. Окончил Политехническую школу в Делфте. Совершенствовал образование в Лейденском и Боннском (у Ф.А. Кекуле) университетах, Высшей медицинской школе в Париже (у Ш.А. Вюрца) и Утрехтском университете (доктор философии, 1874). С 1876 работал в Ветеринарной школе в Утрехте, в 1878-1896 профессор Амстердамского, в 1896-1911 Берлинского университетов.
Один из основателей физической химии и стереохимии. Рассмотрев различные случаи оптической изомерии органических соединений, одновременно с Ж.А. Ле Белем и независимо от него сформулировал (1874) основные положения теории пространственного расположения атомов в молекулах органических соединений, лежащей в основе современной стереохимии. Выдвинул идеи о направленности единиц сродства атома углерода по углам тетраэдра, о наличии двух стереоизомеров у соединения, содержащего атом углерода с четырьмя разными заместителями, и о рёберном соединении тетраэдров при наличии двойной связи. Предсказал изомерию алленовых соединений. Вывел правило, по которому молекулярное вращение соединения с несколькими асимметрическими центрами представляет собой алгебраическую сумму долей молекулярных вращений асимметрических центров, так называемых ротофоров (принцип оптической аддитивности Вант-Гоффа). Исследовал (с 1880-х) кинетику реакций и химическое сродство. Предложил классификацию химических реакций. Установил, что при повышении температуры на 10° скорость реакции увеличивается в 2÷ 4 раза (правило Вант-Гоффа). Вывел одно из основных уравнений химической термодинамики – уравнение изохоры, выражающее зависимость константы равновесия от температуры и теплового эффекта, а также уравнение химической изотермы, выражающее зависимость химического сродства от константы равновесия реакции при постоянной температуре. Опубликовал (1884) работу «Очерки химической динамики», в которой сформулировал основные постулаты химической кинетики. Впервые предложил оценивать реакционную способность веществ с помощью константы скорости реакций, что переводило основной тезис структурной химии (о зависимости реакционной способности от строения) на количественные рельсы в рамках химической кинетики. Заложил (1886-1889) основы количественной теории разбавленных растворов, показав, что растворённые вещества аналогичны веществам в газообразном состоянии и что к разбавленным растворам могут быть применены простые законы (включая закон Авогадро). Вывел закон осмотического давления (закон Вант-Гоффа). Распространил (1890) свои представления о растворах на однородные твёрдые смеси, заложив основы теории твёрдых растворов.
Член ряда академий наук и научных обществ. Иностранный член-корреспондент Петербургской АН (с 1895). Нобелевская премия (1901) [2, стр. 87÷ 88].
[10] Ле Шателье Анри Луи (8.C.1850 - 17.IC.1936) - французский физикохимик и металловед, член Парижской АН (с 1907). Родился в Париже. Учился в Политехнической школе (с 1869) и Высшей горной школе в Париже. Затем был горным инженером в Алжире и Безансоне. В 1878-1919 профессор Высшей горной школы и одновременно в 1898-1907 Коллеж де Франс. В 1907-1925 работал в Парижском университете. Исследования относятся к физической химии. Совместно с П.Э.М.Бертло и французским химиком Ф.Малларом занимался (1881-1882) исследованием процессов воспламенения, горения, взрывов и детонации рудничного газа. Предложил оригинальный способ определения теплоёмкостей газов при высоких температурах. Сформулировал (1884) общий закон смещения химического равновесия, согласно которому при внешнем воздействии на равновесную систему химическое равновесие смещается в сторону, противоположную этому воздействию (принцип Ле Шателье). Изучал химические процессы в металлургии. Сконструировал (1886-1889) термоэлектрический пирометр. Исследовал температурный режим процесса кристаллизации систем из двух металлов, а также из двух солей, подтвердив аналогию между растворами и сплавами. Создал (1897) металлографический микроскоп и усовершенствовал методику исследования строения металлов и сплавов. Изучал (1880-1887) свойства и способы приготовления цементов. Изобрёл платинородиевую термопару. Вывел (1894) термодинамическое уравнение, устанавливающее количественную зависимость между растворимостью, температурой процесса растворения и теплотой плавления вещества. Независимо от Ф.Габеранашёл условия синтеза аммиака. Президент Французского химического общества (1931). Член многих академий наук и научных обществ. Иностранный член-корреспондент Петербургской АН (с 1913) и почётный член АН СССР (с 1926). [2, стр. 263]
[11] Аррениус Сванте Август (19.II.1859-2.C.1927). Шведский физикохимик, член Королевской шведской АН (с 1901). Родился в имении Вейк (близ Упсалы). Окончил Упсальский университет (1878). В 1881-1883 совершенствовал образование в Физическом институте Королевской шведской АН в Стокгольме. В 1884-1885 работал в Упсальском университете. В 1886 работал в Рижском политехническом институте в лаборатории В.Ф. Оствальда, в 1886-1887 – в университетах Вюрцбурга и Граца, в 1888 – в Амстердамском университете в лаборатории Я.Х. Вант-Гоффа, в 1889 – снова в университете Граца. С 1891 в Стокгольмском университете (с 1895 профессор, с 1897 ректор). В 1905-1927 директор Нобелевского института в Стокгольме.
Один из основоположников физической химии. Основные работы посвящены учению о растворах и кинетике химических реакций. На основании своих исследований (1882-1883), свидетельствовавших об увеличении электрической проводимости и активности растворов при их разбавлении, сформулировал (1884) вывод о самопроизвольном распаде молекул солей в растворе на заряженные частицы – ионы, т.е. высказал идею об электролитической диссоциации. Осуществил (1884-1886) цикл работ по изучению зависимости между химическими свойствами электролитов и их проводимостью и предложил (1887) всесторонне обоснованную теорию электролитической диссоциации, согласно которой активность и степень диссоциации электролитов на ионы уменьшаются с ростом концентрации их растворов. Впервые объяснил (1889) сущность температурной зависимости скорости реакций, выдвинув представления об активных, обладающих избыточной энергией и способных вступать в химическое взаимодействие молекулах, число которых экспоненциально возрастает с ростом температуры. Ввёл понятие энергии активации Δ Е и вывел уравнение зависимости константы скорости реакции от фактора частоты столкновения молекул А, температуры и Δ Е, ставшее одним из основных в химической кинетике (уравнение Аррениуса). Ряд работ посвятил космологии и астрофизике.
Член многих академий наук и научных обществ. Иностранный член-корреспондент Петербургской АН (с 1903). Почётный член АН СССР (с 1926). Нобелевская премия (1903) [2, стр. 21÷ 22].
[12] 1 – в реакции разложения уксусного альдегида в газовой фазе;
2 – в реакции разложения ацетондикарбоновой кислоты в водном растворе [1, стр. 476].
[13] Это одновременно показывает, что при повышении температуры всегда сильнее увеличивается скорость эндотермического направления реакции, так как энергия активации его больше. Этим и объясняется то, что с повышением температуры равновесие всегда смещается в направлении эндотермического процесса и тем в большей степени, чем выше тепловой эффект, т.е. чем больше разница в энергиях активации прямой и обратной реакций [1, стр. 478].
[14] В условиях химической реакции равномерное распределение энергии между всеми степенями свободы молекул не всегда успевает достигаться [1, стр. 479].
[15] Не следует думать, что сильное возрастание скорости каждой реакции с повышением температуры приведёт к тому, что при высоких температурах все реакции будут происходить очень быстро. Наряду с такими реакциями при высоких температурах начинают протекать и медленные процессы с более высокой энергией активации, которые практически не могли происходить при умеренных температурах [1, стр. 480].
[16] В самом деле,, но и, следовательно,. Далее,, но по предыдущему, следовательно, и т.д. [1, стр. 481].