
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Конъюнктивные и дизъюнктивные нормальные формы
|
|
Эквивалентные формулы
ОПРЕДЕЛЕНИЕ, Две формулы пропозициональной логики называются эквивалентными (равносильными), если они принимают одинаковые логические значения при любом наборе значений элементарных высказываний, входящих в эти формулы.
Отношение эквивалентности обладает следующими свойствами:
1) А=А (рефлексивно)
2) Если А=В, то В=А (симметрично)
3) Если А=В и В=С, то А=С (транзитивно)
Теорема (об эквивалентной замене). Если формула A содержит подформулу B, и B = C, то А’=A, где А’ образованна из A заменой B на С.
Доказательство. Индукцией по сложности формулы А, используя очевидные эквивалентности:
Если В=С, то Ø B = Ø C
D& B = D& C, B& D = C& D,
DVB = DVC, BVD = CVD,
D®B = D®C, B®D = C®D,
DÅ B = DÅ C, BÅ D = CÅ D.
Основные тождества (алгебра логики)
1. x®y = Ø xÚ y – удаление импликации
2. x < -> y = xÙ y Ú Ø xÙ Ø y
x < -> y = (Ø xÚ y) Ù (xÚ Ø y) удаление эквивалентности
3. x Å y = Ø xÙ y Ú xÙ Ø y
x Å y = (xÚ y) Ù (Ø xÚ Ø y) удаление сложения по модулю 2
4. Ø (xÙ y)= Ø xÚ Ø y;
Ø (xÚ y)=Ø xÙ Ø y – законы де Моргана
5. xÙ (yÚ z)=(xÙ y)Ú (xÙ z); – дистрибутивность конъюнкции относительно дизъюнкции
6. xÚ (yÙ z)=(xÚ y)Ù (xÚ z) - дистрибутивность дизъюнкции относительно конъюнкции
7. xÙ x=x; xÙ y=yÙ x; xÙ (yÙ z)= (xÙ y)Ù z; – идемпотентность, коммутативность и ассоциативность конъюнкции
8. xÚ x=x; xÚ y=yÚ x; xÚ (yÚ z)= (xÚ y)Ú z; - идемпотентность, коммутативность и ассоциативность конъюнкции
9. xÙ 1=x; xÚ 1=1 - операции с константой 1
10. xÙ 0=0; xÚ 0=x – операции с константой 0
11. xÙ Ø x=0 - закон противоречия
12. xÚ Ø x=1 - закон исключения третьего
13. xÙ (yÚ x)=x; xÚ (yÙ x)=x – законы поглощения
14. Ø Ø x=x – закон двойного отрицания
15. (xÙ y)Ú (Ø xÙ z)= (xÙ y)Ú (Ø xÙ z) Ú (y Ù z) - правило резолюции
(xÙ y)Ú (Ø xÙ y)= y - частный случай – склеивание - расщепление
16. (xÚ y)Ù (Ø xÚ z) = (xÚ y)Ù (Ø xÚ z) Ù (yÚ z) - правило резолюции
(xÚ y)Ù (Ø xÚ y)=y - частный случай – склеивание - расщепление
Конъюнктивные и дизъюнктивные нормальные формы
(КНФ и ДНФ)
Элементарной дизъюнкцией называется дизъюнкция переменных высказываний и (или) их отрицаний.
Например: 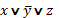
Элементарной конъюнкцией называется конъюнкция переменных высказываний и (или) их отрицаний.
Например: 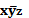
Конъюнктивной нормальной формой (КНФ) данной формулы называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.
Например, выражение 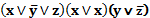 – КНФ.
– КНФ.
Дизъюнктивной нормальной формой (ДНФ) данной формулы называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций.
Например, выражение 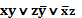 является ДНФ.
является ДНФ.
Для того, чтобы построить по данной формуле алгебры логики равносильную ей ДНФ или КНФ необходимо:
1. Выразить все операции через дизъюнкцию, конъюнкцию и отрицание;
2. Воспользоваться законом де Моргана для того, чтобы отрицания стояли лишь над элементарными переменными высказываниями;
3. Раскрыть скобки (для построения ДНФ) или воспользоваться дистрибутивным законом (для построения КНФ)..
Теорема о тождественной истинности пропозициональной формулы логики. Для того, чтобы формула логики была тождественно истиной, необходимо и достаточно, чтобы каждая элементарная дизъюнкция её конъюнктивной нормальной формы содержала, по крайней мере, одно элементарное переменное высказывание вместе с его отрицанием.
Теорема о тождественной ложности формулы пропозициональной логики. Для того, чтобы формула пропозициональной логики была тождественно ложной (невыполнимой), необходимо и достаточно, чтобы каждая элементарная конъюнкция её ДНФ содержала, по крайней мере, одно элементарное переменное высказывание вместе со своим отрицанием.
Формула пропозициональной логики f называется логическим следствием формул f1, f2, …, fm, если для любых наборов значений переменных, входящих в формулы f1, f2, …, fm, f для которых истины все формулы f1, f2, …, fm, формула f тоже истина. Обозначение f1, f2, …, fm |= f.
Теорема о логическом следствии.Формула пропозициональной логики f является логическим следствием формулы алгебры логики g, тогда и только тогда, если формула g fявляется тавтологией.
|