Симметрические операторы и их свойства.

Квадратичные формы

При изучении аналитической геометрии мы познакомились с элементами теории линий и поверхностей второго порядка. Их уравнения представляли собой алгебраические уравнения второго порядка относительно двух или трех переменных. Здесь мы соприкоснемся с их обобщением на случай n переменных, а так же научимся решать средствами линейной алгебры новые задачи по распознаванию кривых и поверхностей второго порядка. Рассмотрения будем проводить в 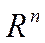рассматриваемом как арифметическое эвклидово пространство со скалярным произведением.

Симметрические операторы и их свойства.

Определение1 Линейный оператор называется симметрическим, если для любых векторов 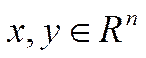выполняется .

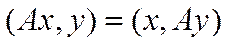Перечислим без доказательства основные свойства симметрических линейных операторов.

1. Линейный оператор является симметрическим тогда и только тогда, когда его матрица в любом базисе симметрична.

2. Собственные векторы симметрического линейного оператора, соответствующие различным собственным значениям, ортогональны.

3. Всякому собственному числу кратности k симметрического оператора соответствует линейно независимая система из k собственных векторов.

4. Для всякого симметрического линейного оператора существует базис в пространстве 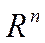, состоящий из его собственных векторов. Последнее означает, что симметрический линейный оператор является оператором простой структуры и в базисе из собственных векторов его матрица имеет диагональный вид.