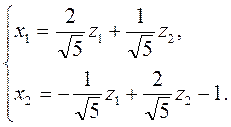Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Запишем матричное уравнение в виде системы линейных уравнений
|
|
А = 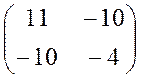 , В =
, В = 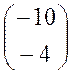 , V =
, V = 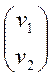 .
.
Запишем матричное уравнение 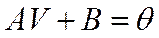 в виде системы линейных уравнений
в виде системы линейных уравнений
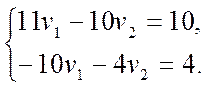
Система крамеровского типа имеет единственное решение 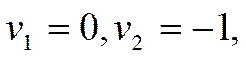 линия имеет единственный центр. После параллельного переноса начала системы координат в этот центр
линия имеет единственный центр. После параллельного переноса начала системы координат в этот центр
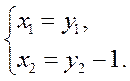
уравнение линии примет вид
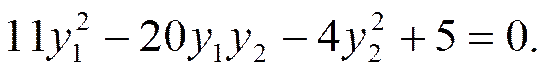
Совершим преобразование Y = QZ (поворот системы координат), приводящее квадратичную форму f = 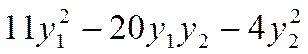 к каноническому виду. В ортонормированном базисе
к каноническому виду. В ортонормированном базисе  двумерного евклидова пространства R 2существует и притом единственный линейный оператор
двумерного евклидова пространства R 2существует и притом единственный линейный оператор  , имеющий в этом базисе матрицу А =
, имеющий в этом базисе матрицу А = 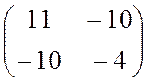 квадратичной формы f. Так как матрица А симметрична, то линейный оператор
квадратичной формы f. Так как матрица А симметрична, то линейный оператор  симетрический и существует ортонормированный базис
симетрический и существует ортонормированный базис  из его собственных векторов. Матрица перехода от базиса
из его собственных векторов. Матрица перехода от базиса  к базису
к базису 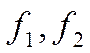 и есть искомая матрица Q.
и есть искомая матрица Q.
Составим и решим характеристическое уравнение матрицы А:
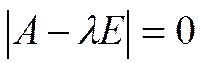 или
или 
Его корни 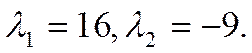 После применения ортогонального преобразования Y = QZ к уравнению
После применения ортогонального преобразования Y = QZ к уравнению 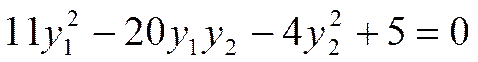 оно примет вид
оно примет вид
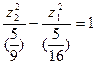 .
.
Это каноническое уравнение гиперболы.
Найдем матрицу Q ортогонального преобразования переменных. Для этого прежде всего надо найти собственный вектор f 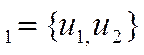 принадлежащий собственному значению
принадлежащий собственному значению 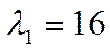 . Ищем ненулевые решения СЛАУ
. Ищем ненулевые решения СЛАУ 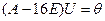 или
или
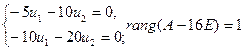 .
.
Общее решение системы 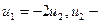 любое число. Фундаментальная система решений состоит из одного вектора, например, f 1 =
любое число. Фундаментальная система решений состоит из одного вектора, например, f 1 = 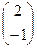 . Пронормировав его, получим
. Пронормировав его, получим 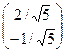 . Аналогично найдем собственный вектор f
. Аналогично найдем собственный вектор f 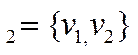 принадлежащий собственному значению
принадлежащий собственному значению  Это, например, f 2 =
Это, например, f 2 = 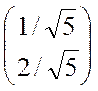 . Векторы
. Векторы 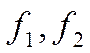 образуют ортонормированный базис R 2, составленный из собственных векторов линейного оператора. Матрица ортогонального преобразования Q составляется из координатных столбцов векторов
образуют ортонормированный базис R 2, составленный из собственных векторов линейного оператора. Матрица ортогонального преобразования Q составляется из координатных столбцов векторов 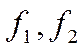 :
:
Q = 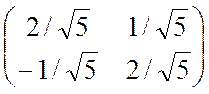 .
.
Выпишем линейное преобразование переменных, приводящее уравнение к каноническому виду