
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные этапы решения задач методом конечных элементов
|
|
Основные понятия и определения
Общая схема метода конечных элементов.
Основные этапы решения задач методом конечных элементов
Метод конечных элементов (МКЭ) – основной метод современной вычислительной механики, лежащий в основе подавляющего большинства современных программных комплексов, предназначенных для выполнения расчетов инженерных конструкций на ЭВМ. МКЭ используется для решения разнообразных задач как в области прочностных расчетов, так и во многих других сферах: гидродинамике, электромагнетизме, теплопроводности и др.
Метод конечных элементов позволяет практически полностью автоматизировать расчет механических систем, хотя, как правило, требует выполнения значительно большего числа вычислительных операций по сравнению с классическими методами механики деформируемого твердого тела. Современный уровень развития вычислительной техники открывает широкие возможности для внедрения МКЭ в инженерную практику. Поэтому знание основ метода конечных элементов и современных программных средств, позволяющих на его основе решать разнообразные задачи, в наше время для инженера является абсолютно необходимым.
В МКЭ исследуемая конструкция мысленно разбивается на отдельные части – конечные элементы, соединяющиеся между собой в узлах. Совокупность соединенных между собой и прикрепленных к основанию конечных элементов образует расчетную схему, называемую конечно-элементной схемой или конечно-элементной моделью.
Каждый отдельно конечный элемент должен быть достаточно простым,
чтобы имелась возможность легко определить перемещения и напряжения в
любой его части по заданным перемещениям узлов. Связь между перемещениями узлов элемента и силами, действующими на них, задается при помощи матрицы жесткости элемента. Количество перемещений узлов элемента, которые однозначно определяют положение данного элемента, называют числом степеней свободы элемента.
Аналогично, для всей конечно-элементной схемы вводятся матрица жесткости системы K, или глобальная матрица жесткости, устанавливающая связь между перемещениями узлов системы и силами, действующими на них, а также число степеней свободы системы, или глобальное число степеней свободы – количество координат узлов системы, которые достаточно знать, чтобы однозначно определить положение всей системы. Обычно, все степени свободы представляются в виде вектора U, называемого вектором узловых перемещений.
Матрица жесткости системы формируется из матриц жесткости элементов. В программных комплексах, реализующих алгоритм метода конечных элементов, эти матрицы для элементов различных типов хранятся в готовом виде. Матрицы жесткости элементов могут формироваться и храниться в памяти ЭВМ в своих локальных системах осей координат. Матрица жесткости системы формируется в единой системе координат, называемой глобальной системой осей координат.
Так как матрица жесткости системы устанавливает связь между силами, приложенными к ее узлам, и перемещениями ее узлов, то, имея построенную матрицу жесткости системы и зная узловую нагрузку F, можно найти перемещения всех узлов конечно-элементной схемы. Для этого требуется решить систему линейных алгебраических уравнений вида:
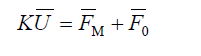
Здесь Fм – вектор внешних сил, а F0 – есть узловой вектор начальных сил, который имеет место, например, при учете начальных температурных напряжений.
Порядок этой системы равен глобальному числу степеней свободы системы. По вычисленным таким образом перемещениям определяются напряжения и деформации.
Физический смысл векторов U и F определяются областью применения МКЭ в соответствии с таблицей:
Физический смысл векторов U и F в различных конечно-элементных приложениях 
Основные этапы решения задач с применением МКЭ могут быть представлены в виде схемы (рисунок 1.1).
| Рисунок 1.1 – Основные этапы 1 |
 Первая стадия – геометрическое моделирование включает создание геометрии модели конструкции, пригодной для МКЭ, с учетом всех параметров, которые могут оказать существенное влияние на результаты расчетов. На этой стадии помимо ввода геометрических параметров конструкции задаются физические свойства материалов, из которых она изготовлена.
Первая стадия – геометрическое моделирование включает создание геометрии модели конструкции, пригодной для МКЭ, с учетом всех параметров, которые могут оказать существенное влияние на результаты расчетов. На этой стадии помимо ввода геометрических параметров конструкции задаются физические свойства материалов, из которых она изготовлена.
На этапе создания сетки конечных элементов выясняется целесообразность использования различных видов конечных элементов(оболочечных, балочных, пластин, объемных
и т. д.) в рассматриваемой модели. На этойстадии выполняются мероприятия по созданию максимально возможного количества областей с регулярной сеткой конечных элементов. В местах, где предполагаются большие
градиенты напряжений, необходима более мелкая сетка.
На стадии моделирования граничных условий учитывают как действие активных сил, так и наложенных на систему связей. Приложение силовых факторов должно учитывать особенности реальной работы конструкции при рассматриваемых режимах эксплуатации.
Количество связей должно быть достаточным, чтобы обеспечить построение кинематически неизменяемой модели.
Численное решение системы уравнений равновесия выполняется, как правило, автоматически с использованием ЭВМ.
На пятом этапе проводят анализ полученных результатов путем получения полей законов распределения напряжений и деформаций, а также построения необходимых графических зависимостей либо табличных форм вывода результатов.