
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Атрибуты конечных элементов и построение сетки
|
|
В процессе конечно-элементного моделирования одним из важных этапов является создание сетки конечных элементов. Рассмотрим основные типы конечных элементов и их свойства, называемые атрибутами элементов.
1. Собственная размерность. Положения конечных элементов могут описываться одной, двумя или тремя пространственными координатами в зависимости от размерности задачи. Соответствующее число внутренних или локальных координат называется собственной размерностью элемента. Время в динамическом анализе рассматривается как дополнительная размерность. Отметим, что иногда в расчетах используются специальные элементы с нулевой размерностью, такие как точечные массы или сосредоточенные упругие элементы (пружины).
2. Узловые точки. Узловые точки, или узлы предназначены для описания геометрии элемента и задания физических степеней свободы (числа неизвестных функций). Как правило, узлы находятся в угловых или крайних точках элемента. Иногда вводят дополнительные узлы, расположенные внутри элемента. Число узлов связано с порядком аппроксимации, который обеспечивает данный конечный элемент. Элементы, имеющие только угловые узлы, называются линейными и обеспечивают линейную интерполяцию геометрии и функций. Элементы, имеющие дополнительные узлы на своих границах между угловыми точками, могут обеспечивать квадратичную или даже кубическую интерполяцию (рисунок 1.2). При наличии современных автоматических генераторов конечно-элементных сеток часто бывает проще и удобнее разбить конструкцию на большое число линейных элементов простой формы, чем использовать элементы высокого порядка, требующие для построения сетки значительной работы вручную. В то же время квадратичная и кубическая интерполяции обеспечивают более высокую точность расчета.
3. Геометрия элемента. Геометрия элемента определяется расположением узловых точек. Большинство элементов, используемых в расчетах, имеют простую геометрическую форму. Например, в одномерном случае элементы обычно представляют собой прямолинейные отрезки или сегменты кривых линий; в двумерном случае элементы имеют трех- или четырехстороннюю форму (см. рисунок 1.2); в трехмерных задачах наиболее распространены такие геометрические фигуры, как тетраэдры, гексаэдры (см. рисунок 1.2) и призмы.
4. Степени свободы. В качестве степеней свободы могут фигурировать как узловые значения неизвестной функции, так и ее производные по пространственным координатам в узлах. В первом случае элементы относятся к типу лагранжевых элементов, во втором – эрмитовых. Например, в простейшей задаче о растяжении стержня неизвестной функцией являются продольные смещения узлов стержня. Соответственно в качестве степеней свободы выступают узловые значения данной функции и, следовательно, конечный элемент относится к лагранжевому типу. Наоборот, в задаче об изгибе стержня неизвестной функцией являются поперечные смещения узлов центральной оси стержня, а в качестве степеней свободы используются как узловые значения самой функции, так и ее производной по продольной координате. Таким образом, конечный элемент, применяемый в расчетах стержня на изгиб, относится к типу эрмитовых элементов. Заметим также, что данные обозначения происходят от названий полиномов Лагранжа и Эрмита, широко используемых в прикладной математике для интерполяции функций по узловым значениям.

5. Определяющие соотношения. Для конечных элементов, используемых в механических расчетах, определяющее соотношение задает поведением материала, из которого изготовлена конструкция. Например, в качестве такого соотношения во многих случаях используется обобщенный закон Гука, связывающий тензоры деформаций и напряжений в точке. Для линейного упругого стержневого элемента достаточно задать один модуль Юнга E и коэффициент температурного расширения.
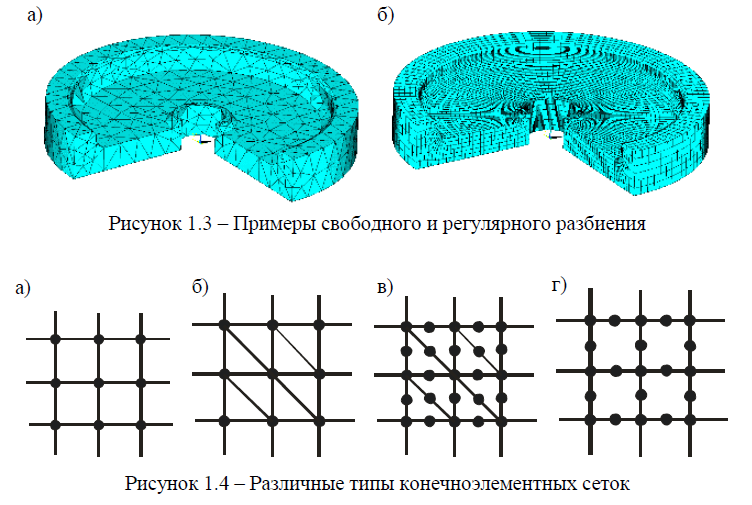
6. Свойства сечения. К свойствам сечения относятся площади и моменты инерции одномерных конечных элементов (балки, стержни), а также толщины двумерных конечных элементов (пластины, оболочки). Одним из наиболее важных этапов конечно-элементного анализа является построение сетки конечных элементов. В существующих программных комплексах, как правило, предусматриваются два основных метода: построение произвольной сетки (рисунок 1.3, а) и построение упорядоченной сетки (рисунок 1.3, б).Необходимо помнить, что точность расчета с помощью МКЭ зависит от правильного выбора типов и размеров конечных элементов. Практика расчетов с применением МКЭ позволяет дать следующие рекомендации:
– линейные элементы требуют более мелкой сетки, чем элементы более высокого порядка (с промежуточными узлами);
– упорядоченная сетка предпочтительнее произвольной;
– прямоугольная сетка с четырьмя узлами (рисунок 1.4, а) более выгодна, чем сетка с треугольными элементами (рисунок 1.4, б);
– сетка треугольных элементов с промежуточными узлами (рисунок 1.4, в) имеет точность, близкую к сетке прямоугольных элементов с четырьмя узлами (см. рисунок 1.4, а);
– прямоугольная сетка с восемью узлами (рисунок 1.4, г) предпочтительнее сетке треугольных элементов с промежуточными узлами (см. рисунок 1.4, в), несмотря на большую площадь прямоугольных элементов;
– аппроксимация смещений кубическим полиномом (элемент третьегопорядка) не требует мелкой сетки.
Мелкая сетка требуется там, где ожидается большой градиент деформаций или напряжений (отверстие, выточка, трещина и т. п.). В то же время крупная сетка может применяться в зонах с мало изменяющимися относительными деформациями или напряжениями, а также в областях, не представляющих особого интереса для расчетчика. В связи с этим перед созданием конечно-элементной сетки необходимо выделить предполагаемые области концентрации напряжений.
Заметим, что точность результатов расчетов уменьшается, если существенно различаются размеры соседних элементов вблизи концентратора напряжений (рисунок 1.5).
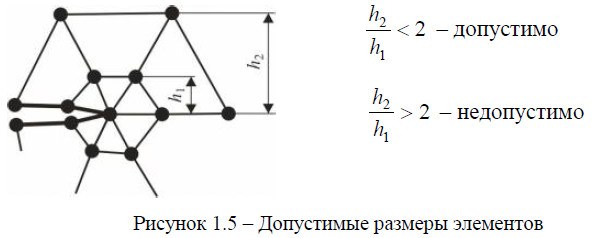
Форма конечных элементов также влияет на точность вычислений. Следует избегать слишком вытянутых элементов, так как элементы с примерно одинаковыми размерами сторон дают меньшую ошибку (рисунок 1.6, а). Запрещается использовать четырехугольные элементы с углами, превышающими 180° (рисунок 1.6, б).
