Листинг 3.4

#include “stdafx.h”

#include < iostream>

#include < math.h>

using namespace std;

const double x_min = -10.;

const double x_max = 10.;

const int N = 100;

int _tmain(int argc, _TCHAR* argv[])

{

double y, dx = (x_max - x_min) / N;

for(double x = x_min; x < = x_max; x += dx)

{

if(x < = 0.) y = 2*x*x + cos(x);

else if(x < 5.) y = x + 1;

else y = sin(2*x) - x*x;

cout < < “x = “ < < x < < “ y = “ < < y < < endl;

}

getch();

}

Любой из трех параметров цикла forможет быть опущен. Например, найти сумму натуральных чисел от 1 до 10 можно с помощью следующего фрагмента программы:

for(S = 0, i = 1; i < 11)

{

S += i;

i++;

}

Если не задано условие завершения в цикле for, то он будет выполняться бесконечно. В этом случае для завершения работы цикла необходимо использовать оператор break. Для нахождения суммы чисел от 1 до 10 можно использовать также следующий фрагмент кода:

for(S = 0, i = 1;; i++)

{

if(i > 10) break;

S += i;

}

Также может быть пропущен список инициализации в цикле for, в этом случае:

S = 0;

i = 1;

for(; i < 11; i++) S += i;

При выполнении итерационного цикла for условие продолжения может изменяться либо при вычислении его значений, либо под действием операторов тела цикла, либо под действием выражений из списка заголовка. Если условие продолжения не изменяется, либо отсутствует, то цикл бесконечен. Следующие операторы обеспечивают бесконечное выполнение пустых операторов:

for(;;); \\ бесконечный цикл

for(; 1;); \\ бесконечный цикл

Цикл с предусловием или цикл типа while. Не всегда число повторений цикла известно заранее, в этих случаях применяются циклы с предусловием (проверка перед циклом) или с постусловием (проверка после цикла) - это цикл while. Основная его форма

while(< выражение_условие>) < тело_цикла>

При входе в цикл вычисляется выражение_условие. Если его значение отлично от нуля, то выполняется тело_цикла. Затем вычисление условия, заданного в выражении_условии и выполнение операторов тела_цикла выполняются последовательно, пока выражение_условие не станет равным 0. Данная инструкция может быть выполнена ноль или более раз. Оператором while удобно пользоваться для просмотра всевозможных последовательностей, если в конце каждой из них находится заранее известный признак.

Например, сумма натуральных чисел от 1 до 10 с использованием цикла while может быть найдена следующим образом:

S = 0;

i = 1;

while(i < = 10)

{

S += i;

i++;

}

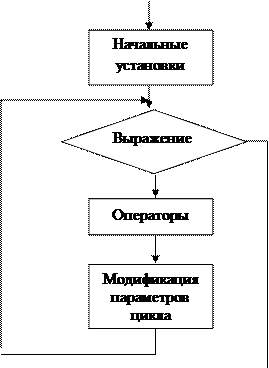Рисунок 3.6 – Структурная схема оператора цикла с предусловием

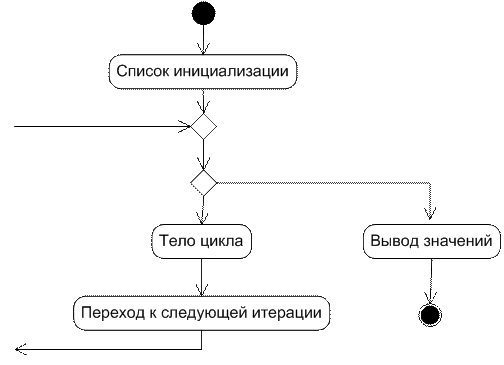
Рисунок 3.7 - Фрагмент диаграммы деятельности UML, описывающей действия оператора while в C++

Пример 3.4. Найти значение натурального логарифма 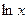от аргумента , значение которого вводится с клавиатуры с точностью 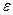, по его разложению в ряд

.

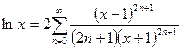(3.3)

Чтобы вычислить сумму ряда найдем рекуррентное соотношение, позволяющее найти следующий член ряда, исходя из значения текущего. Для этого разделим следующий член ряда на текущий. Текущий член ряда задается выражением

,

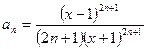(3.4)

тогда как следующий член ряда может быть определен следующим образом

.

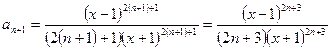(3.5)

Отношение следующего и текущего членов ряда

,

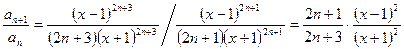(3.6)

следовательно

.

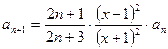(3.7)

Первый член ряда

.

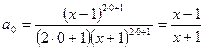(3.8)

С учетом выражения (3.8) формула (3.7) может быть записана в следующем виде

.

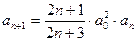(3.9)

Условие завершения вычисления суммы ряда может быть записано следующим образом 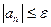. На основании данных рассуждений может быть построена диаграмма деятельности UML для решения поставленной задачи (рис. 3.8)

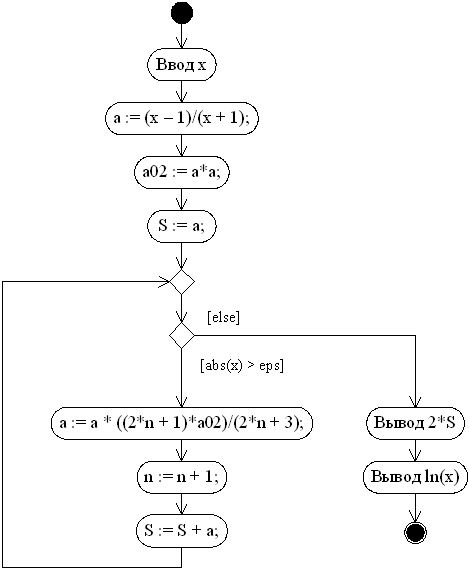
Рисунок 3.8 - UML-диаграмма деятельности для расчета значения натурального логарифма по его разложению в ряд

По составленной диаграмме может быть написана программа вычисления значения натурального логарифма по его разложению в бесконечный ряд.