Эйлерово описание движения сплошной среды

Пусть нас интересует не история движения индивидуальных материальных точек сплошной среды, а то, что происходит в разные моменты времени в каждой геометрической точке пространства, связанной с системой отсчета наблюдателя. При этом, через фиксированные точки пространства проходят резине материальные частицы. Такое рассмотрение движения континуума и представляет эйлерово описание движения.

Аналогия с потоком автомобилей. Лагранжево описание – описание с точки зрения водителей (координаты, скорости, температура и другие характеристики каждого автомобиля). Эйлерово описание – описание с точки зрения регулировщиков (скорости и другие характеристики автомобилей в различных (фиксированных и контролируемых) точках дорог.

Таким образом, при эйлеровом описании все характеристики континуума задаются в виде функций от координат точек пространства x1, x2,, x3 и времени t:

v = v(x1, x2,, x3, t), T = T(x1, x2,, x3, t). (2.4.1)

Координаты точек пространства x1, x2,, x3 и время t называются эйлеровыми переменными

Субстанциональная (индивидуальная) и частная (локальная) производные по времени. В механике сплошной среды используют различные производные по времени.

Определение: Скорость изменения какого-либо параметра, например ϕ, для фиксированной материальной частицы (перемещающейся в пространстве) в соответствие с полем скорости v = v(x1, x2,, x3, t) при эйлеровом описании или полем скорости vk = vk(ξ 1, ξ 2, ξ 3, t) при лагранжевом описании называется субстанциональной (substantional derivative) полной или индивидуальной производной по времени и обозначается через

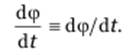
1. Если имеем лагранжево описание (2.3.17) для Т и r:

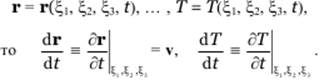
2. Если имеем эйлерово описание (2.4.1)

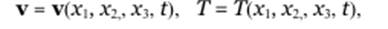
то вычисление dT/dt и dv/dt несколько осложняется. Перейдем от эйлеровых переменных к лагранжевым

Дифференцируя эти сложные фикции по t, имеем

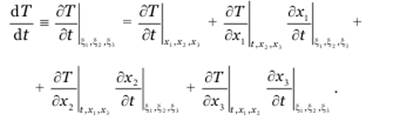
Учитывая, что (dxi/dt)ξ, 1ξ 2, ξ 3≡ dxi/dt в соответствии с (2.3.12) определяют компоненты скорости материальных частиц, имеем

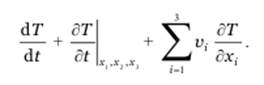
В дальнейшем под ∂ /∂ t если нет специальной оговорки, подразумевается частная производная (partial derivative) по t в эйлеровым переменных. Тогда используя правила немого суммирования, получим

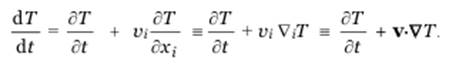
Аналогично для ускорения материальной частицы получим

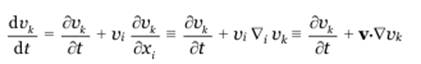
или в векторной форме

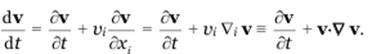
Нетрудно доказать, что если Т и v соответственно скаляр и вектор, то 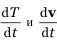являются скаляром и вектором.

Субстанциональная производная по времени 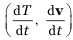характеризующая изменение Т и v в индивидуальной материальной частице, в эйлеровых переменных равна локальной или частной производной 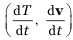, характеризующей изменение Т и v в фиксированной точке пространства, плюс так называемая конвективная производная (vi ∇ i Т и vj ∇ j v), характеризующая изменение и из-за перемещения материальной частицы.

Когда вклад конвективной производной равен нулю (v ∇ Т = 0)?

Это имеет место в трех случаях:

1) v = 0 – нет движения;

2) ∇ T = 0 – однородное;

3) v ⊥ ∇ T – течение вдоль поверхности уровня поля Т.

В частности, ускорение a(x, t) при эйлеровом описании находится по формуле
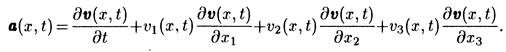