Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многоэлектронные атомы
|
|
Принцип Паули. Распределение электронов в атоме по состояниям. Периодическая система элементов Д.И. Менделеева.
Если тождественные частицы имеют одинаковые квантовые числа, то их волновая функция симметрична относительно перестановки частиц. Отсюда следует, что два одинаковых фермиона, входящих в одну систему, не могут находиться в одинаковых состояниях, так как для фермионов волновая функция должна быть антисимметричной. Обобщая опытные данные, В. Паули сформулировал принцип, согласно которому системы фермионов встречаются в природе только в состояниях, описываемых антисимметричными волновыми функциями (квантово-механическая формулировка принципа Паули).
Из этого положения вытекает более простая формулировка принципа Паули, которая и была введена им в квантовую теорию (1925) еще до построения квантовой механики: в системе одинаковых фермионов любые два из них не могут одновременно находиться в одном и том же состоянии. Отметим, что число однотипных бозонов, находящихся в одном и том же состоянии, не лимитируется.
Напомним, что состояние электрона в атоме однозначно определяется набором четырех квантовых чисел:
главного n (n =1, 2, 3,...),
орбитального l (l = 0, 1, 2,..., n—1),
магнитного ml (ml = - l,.... - 1, 0, +1,..., + l),
магнитного спинового (ms = + 1/2, - 1/2).
Распределение электронов в атоме подчиняется принципу Паули, который может быть использован в его простейшей формулировке: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел n, l, ml и ms, т. е.
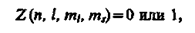
Совокупность электронов в многоэлектронном атоме, имеющих одно и то же главное квантовое число n, называют электронной оболочкой. В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному l. Поскольку.орбитальное квантовое число принимает значения от 0 до n - 1, число подоболочек равно порядковому номеру nоболочки. Количество электронов в подоболочке определяется магнитным и магнитным спиновым квантовыми числами: максимальное число электронов в подоболочке с данным l равно 2(2 l + 1). Обозначения оболочек, а также распределение электронов по оболочкам и подоболочкам представлены в табл. 6.
Таблица 6
| Главное квантовое число л | |||||||||||||||
| Символ оболочки | К | L | M | N | О | ||||||||||
| Максимальное число электронов в оболочке | |||||||||||||||
| Орбитальное квантовое число l | |||||||||||||||
| Символ подоболочки | 1s | 2s | 2р | 3s | 3р | 3d | 4s | 4р | 4d | 4f | 5s | 5p | 5d | 5f | 5g |
| Максимальное число электронов в подоболочке |
Принцип Паули, лежащий в основе систематики заполнения электронных состояний в атомах, позволяет объяснить Периодическую систему элементов Д. И. Менделеева (1869) — фундаментального закона природы, являющегося основой современной химии, атомной и ядерной физики.
Д. И. Менделеев ввел понятие порядкового номера Z химического элемента, равного числу протонов в ядре и соответственно общему числу электронов в электронной оболочке атома. Расположив химические элементы по мере возрастания порядковых номеров, он получил периодичность в изменении химических свойств элементов.
Рентгеновские спектры. Природа сплошного и характеристического рентгеновских спектров. Объяснить закон Мозли. Записать на основе этого закона формулу для частоты 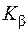 -линии характеристического спектра
-линии характеристического спектра
Большую роль в выяснении строения атома, а именно распределения электронов по оболочкам, сыграло излучение, открытое в 1895 г. немецким физиком В. Рентгеном (1845—1923) и названное рентгеновским. Самым распространенным источником рентгеновского излучения является рентгеновская трубка, в которой сильно ускоренные электрическим полем электроны бомбардируют анод (металлическая мишень из тяжелых металлов, например W или Pt), испытывая на нем резкое торможение. При этом возникает рентгеновское излучение, представляющее собой электромагнитные волны с длиной волны примерно 1012 —10-8 м. Волновая природа рентгеновского излучения доказана опытами по его дифракции, рассмотренными в § 182.
Исследование спектрального состава рентгеновского излучения показывает, что его спектр имеет сложную структуру (рис. 306) и зависит как от энергии электронов, так и от материала анода. Спектр представляет собой наложение сплошного спектра, ограниченного со стороны коротких длин волн некоторой границей lmin, называемой границей сплошного спектра, и линейчатого спектра — совокупности отдельных линий, появляющихся на фоне сплошного спектра.

Исследуя рентгеновские спектры элементов, английский физик Г. Мозли (1887—1915) установил в 1913 г. соотношение, называемое законом Мозли:
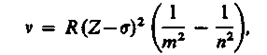 (229.2)
(229.2)
где v — частота, соответствующая данной линии характеристического рентгеновского излучения, R— постоянная Ридберга, s— постоянная экранирования, m = 1, 2, 3,... (определяет рентгеновскую серию), nпринимает целочисленные значения начиная с от +1 (определяет отдельную линию соответствующей серии). Закон Мозли (229.2) подобен обобщенной формуле Бальмера (209.3) для атома водорода.
Смысл постоянной экранирования заключается в том, что на электрон, совершающий переход, соответствующий некоторой пинии, действует не весь заряд ядра Ze, а заряд (Z - s)e, ослабленный экранирующим действием других электронов. Например, для Кa-линии s = 1, и закон Мозли запишется в виде