Элементы квантовой статистики и физики твердого тела

Элементы зонной теории кристаллов. Энергетические зоны в кристаллах. Валентная зона и зона проводимости. Заполнение зон: металлы, диэлектрики, полупроводники.

Зонная теория твердых тел позволила с единой точки зрения истолковать существование металлов, диэлектриков и полупроводников, объясняя различие в их электрических свойствах, во-первых, неодинаковым заполнением электронами разрешенных зон и, во-вторых, шириной запрещенных зон.

Степень заполнения электронами энергетических уровней в зоне определяется заполнением соответствующих атомных уровней. Если при этом какой-то энергетический уровень полностью заполнен, то образующаяся энергетическая зона также запол нена целиком. В общем случае можно говорить о валентной зоне, которая полностью заполнена электронами и образована из энергетических уровней внутренних электронов свободных атомов, и о зове проводимости (свободной зоне), которая либо частично заполнена электронами, либо свободна и образована из энергетических уровней внешних «коллективизированных» электронов изолированных атомов.

В зависимости от степени заполнения зон электронами и ширины запрещенной зоны возможны четыре случая, изображенные на рис. 314.

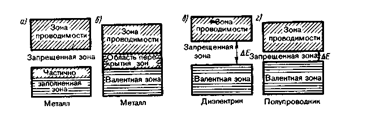
На рис. 314, а самая верхняя зона, содержащая электроны, заполнена лишь частично, т. е. в ней имеются вакантные уровни. В данном случае электрон, получив сколь угодно малую энергетическую «добавку» (например, за счет теплового движения или электрического поля), сможет перейти на более высокий энергетический уровень той же зоны, т. е. стать свободным и участвовать в проводимости. Внутривенный переход вполне возможен, так как, например, при 1 К энергия теплового движения kT» 10^-4 эВ, т. е. гораздо больше разности энергий между соседними уровнями зоны (примерно 10^-22 эВ). Таким образом, если в твердом теле имеется зона, лишь частично заполненная электронами, то это тело всегда будет проводником электрического тока. Именно это свойственно металлам.

Твердое тело является проводником электрического тока и в том случае, когда валентная зона перекрывается свободной зоной, что в конечном счете приводит к не полностью заполненной зоне (рис. 314, б). Это имеет место для щелочно-земельных элементов, образующих II группу таблицы Менделеева (Be, Mg, Ca, Zn,...). В данном случае образуется так называемая «гибридная» зона, которая заполняется валентными электронами лишь частично. Следовательно, в данном случае металлические свойства щелочно-земельных элементов обусловлены перекрытием валентной и свободной зон.

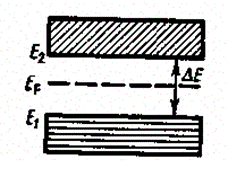
Помимо рассмотренного выше перекрытия зон возможно также перераспределение электронов между зонами, возникающими из уровней различных атомов, которое может привести к тому, что вместо двух частично заполненных зон в кристалле окажутся одна полностью заполненная (валентная) зона и одна свободная зона (зона проводимости). Твердые тела, у которых энергетический спектр электронных состояний состоит только из валентной зоны и зоны проводимости, являются диэлектриками или полупроводниками в зависимости от ширины запрещенной зоны DE.

Если ширина запрещенной зоны кристалла порядка нескольких электрон-вольт, то тепловое движение не может перебросить электроны из валентной зоны в зону проводимости и кристалл является диэлектриком, оставаясь им при всех реальных температурах (рис. 314, в). Если запрещенная зона достаточно узка (DЕ порядка 1 эВ), то переброс электронов из валентной зоны в зону проводимости может быть осуществлен сравнительно легко либо путем теплового возбуждения, либо за счет внешнего источ ника, способного передать электронам энергию DЕ, и кристалл является полупроводником (рис. 314, г).

Электропроводность металлов. Носители тока в металлах. Недостаточность классической электронной теории.

Квантовая теория электропроводности металлов — теория электропроводности, основывающаяся на квантовой механике и квантовой статистике Ферми — Дирака, — пересмотрела вопрос об электропроводности металлов, рассмотренный в классической физике. Расчет электропроводности металлов, выполненный на основе этой теории, приводит к выражению для удельной электрической проводимости металла

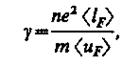
которое по внешнему виду напоминает классическую формулу (103.2) для g, но имеет совершенно другое физическое содержание. Здесь n— концентрация электронов проводимости в металле, á l _Fñ — средняя длина свободного пробега электрона, имеющего энергию Ферми, á u_Fñ — средняя скорость теплового движения такого электрона.

Выводы, получаемые на основе формулы (238.1), полностью соответствуют опытным данным. Квантовая теория электропроводности металлов, в частности, объясняет зависимость удельной проводимости от температуры: g~ 1/T(классическая теория (см. § 103) дает, что g ~ 1/Ö T, а также аномально большие величины (порядка сотен периодов решетки) средней длины свободного пробега электронов в металле (см. § 103).

Квантовая теория рассматривает движение электронов с учетом их взаимодействия с кристаллической решеткой. Согласно корпускулярно-волновому дуализму, движению электрона сопоставляют волновой процесс. Идеальная кристаллическая решетка (в ее узлах находятся неподвижные частицы и в ней отсутствуют нарушения периодичности) ведет себя подобно оптически однородной среде — она «электронные волны» не рассеивает. Это соответствует тому, что металл не оказывает электрическому току — упорядоченному движению электронов — никакого сопротивления. «Электронные волны», распространяясь в идеальной кристаллической решетке, как бы огибают узлы решетки и проходят значительные расстояния.

В реальной кристаллической решетке всегда имеются неоднородности, которыми могут быть, например, примеси, вакансии; неоднородности обусловливаются также тепловыми колебаниями. В реальной кристаллической решетке происходит рассеяние «электронных волн» на неоднородностях, что и является причиной электрического сопротивления металлов. Рассеяние «электронных волн» на неоднородностях, связанных с тепловыми колебаниями, можно рассматривать как столкновения электронов с фононами.

Согласно классической теории, á u_Fñ ~ Ö T, поэтому она не смогла объяснить истинную зависимость у от температуры. В квантовой теории средняя скорость á u_Fñ от температуры практически не зависит, так как доказывается, что с изменением температуры уровень Ферми остается практически неизменным. Однако с повышением температуры рассеяние «электронных волн» на тепловых колебаниях решетки (на фононах) возрастает, что соответствует уменьшению средней длины свободного пробега электронов. В области комнатных температур á l _Fñ ~ Т^-1, поэтому, учитывая независимость á uñ от температуры, получим, что сопротивление металлов (R ~ l/g)в соответствии с данными опытов растет пропорционально Т. Таким образом, квантовая теория электропроводности металлов устранила и эту трудность классической теории.

Собственная проводимость полупроводников. Примесная проводимость полупроводников. P - n переход и его свойства.

Собственными полупроводниками являются химически чистые полупроводники, а их проводимость называется собственной проводимостью. Примером собственных полупроводников могут служить химически чистые Ge, Se, а также многие химические соединения: InSb, GaAs, CdS и др.

При 0 К и отсутствии других внешних факторов собственные полупроводники ведут себя как диэлектрики. При повышении же температуры электроны с верхних уровней валентной зоны I могут быть переброшены на нижние уровни зоны проводимости II (рис. 315). При наложении на кристалл электрического поля они перемещаются против поля и создают электрический ток. Таким образом, зона II из-за ее частичного «укомплектования» электронами становится зоной проводимости. Проводимость собственных полупроводников, обусловленная электронами, называется электронной проводимостью или проводимостью n-тнпа (от лат. negative — отрицательный).

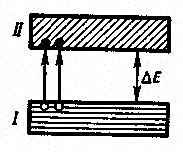
Рис. 315

В результате тепловых забросов электронов из зоны I в зону II в валентной зоне возникают вакантные состояния, получившие название дырок. Во внешнем электрическом поле на освободившееся от электрона место — дырку — может переместиться электрон с соседнего уровня, а дырка появится в том месте, откуда ушел электрон, и т. д. Такой процесс заполнения дырок электронами равносилен перемещению дырки в направлении, противоположном движению электрона, так, как если бы дырка обладала положительным зарядом, равным по величине заряду электрона. Проводимость собственных полупроводников, обусловленная квазичастицами — дырками, называется дырочной проводимостью или проводимостью р-типа (от лат. positive — положительный).

Таким образом, в собственных полупроводниках наблюдаются два механизма проводимости: электронный и дырочный. Число электронов в зоне проводимости равно числу дырок в валентной зоне, так как последние соответствуют электронам, возбужденным в зону проводимости. Следовательно, если концентрации электронов проводимости и дырок обозначить соответственно n_е и n_р, то

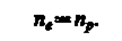(242.1)

Проводимость полупроводников всегда является возбужденной, т. е. появляется только под действием внешних факторов (температуры, облучения, сильных электрических полей и т. д.).

В собственном полупроводнике уровень Ферми находится в середине запрещенной зоны (рис. 316).

Проводимость полупроводников, обусловленная примесями, называется примесной проводимостью, а сами полупроводники — примесными полупроводниками. Примесная проводимость обусловлена примесями (атомы посторонних элементов), а также дефектами типа избыточных атомов (по сравнению со стехиометрическим составом), тепло выми (пустые узлы или атомы в междоузлиях) и механическими (трещины, дислокации и т. д.) дефектами. Наличие в полупроводнике примеси существенно изменяет его проводимость. Например, при введении в кремний примерно 0, 001 ат.% бора его проводимость увеличивается примерно в 10^б раз.

В полупроводниках с примесью, валентность которой на единицу больше валентности основных атомов, носителями тока являются электроны; возникает электронная примесная проводимость (проводимость n-тнпа). Полупроводники с такой проводимостью называются электронными (или полупроводниками n-тнпа). Примеси, являющиеся источником электронов, называются донорами, а энергетические уровни этих примесей — донорнымн уровнями.

В полупроводниках с примесью, валентность которой на единицу меньше валентности основных атомов, носителями тока являются дырки; возникает дырочная проводимость (проводимость р-типа).Полупроводники с такой проводимостью называются дырочными (или полупроводниками р-типа).Примеси, захватывающие электроны из валентной зоны полупроводника, называются акцепторами, а энергетические уровни этих примесей — акцепторными уровнями.

В отличие от собственной проводимости, осуществляющейся одновременно электронами и дырками, примесная проводимость полупроводников обусловлена в основном носителями одного знака: электронами — в случае донорной примеси, дырками — в случае акцепторной. Эти носители тока называются основными. Кроме основных носителей в полупроводнике имеются и неосновные носители: в полупроводниках n-типа — дырки, в полупроводниках р-типa — электроны.

Наличие примесных уровней в полупроводниках существенно изменяет положение уровня Ферми Е_F. Расчеты показывают, что в случае полупроводников n-типа уровень Ферми Е_{F 0} при 0 К расположен посередине между дном зоны проводимости и донорным уровнем (рис. 321).

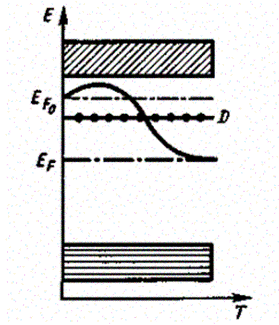
Рис. 321

С повышением температуры все большее число электронов переходит из донорных состояний в зону проводимости, но, помимо этого, возрастает и число тепловых флуктуации, способных возбуждать электроны из валентной зоны и перебрасывать их через запрещенную зону энергий. Поэтому при высоких температурах уровень Ферми имеет тенденцию смещаться вниз (сплошная кривая) к своему предельному положению в центре запрещенной зоны, характерному для собственного полупроводника.

Уровень Ферми в полупроводниках р-типа при 0 К Е_F0располагается посередине между потолком валентной зоны и акцепторным уровнем (рис. 322). Сплошная кривая опять-таки показывает его смещение с температурой. При температурах, при которых примесные атомы оказываются полностью истощенными и увеличение концентрации носителей происходит за счет возбуждения собственных носителей, уровень Ферми располагается посередине запрещенной зоны, как в собственном полупроводнике.

Граница соприкосновения двух полупроводников, один из которых имеет электронную, а другой — дырочную проводимость, называется электронно-дырочным переходом (или p-n-нереходом). Эти переходы имеют большое практическое значение, являясь основой работы многих полупроводниковых приборов. p-n-Переход нельзя осуществить просто механическим соединением двух полупроводников.

Рассмотрим физические процессы, происходящие в p-n-переходе (рис. 336).

Рис. 336

Пусть донорный полупроводник (работа выхода — А_n, уровень Ферми — Е_Fn)приводится в контакт (рис. 336, б) сакцепторным полупроводником (работа выхода — А_р, уровень Ферми — Е_Fp). Электроны из n-полупроводника, где их концентрация выше, будут диффундировать в p-полупроводник, где их концентрация ниже. Диффузия же дырок происходит в обратном направлении — в направлении р®n.

В n-полупроводнике из-за ухода электронов вблизи границы остается нескомпенсированный положительный объемный заряд неподвижных ионизованных донорных атомов. В n-полупроводнике из-за ухода дырок вблизи границы образуется отрицательный объемный заряд неподвижных ионизованных акцепторов (рис. 336, а). Эти объемные заряды образуют у границы двойной электрический слой, поле которого, направленное от n-области к p-области, препятствует дальнейшему переходу электронов в направлении n®ри дырок в направлении р®n.Если концентрации доноров и акцепторов в полупроводниках n- и р-типаодинаковы, то толщины слоев d₁ и d₂(рис. 336, в), в которых локализуются неподвижные заряды, равны (d₁ = d₂).

При определенной толщине p-n-перехода наступает равновесное состояние, характеризуемое выравниванием уровней Ферми для обоих полупроводников (рис. 336, в). В области p-n-перехода энергетические зоны искривляются, в результате чего возникают потенциальные барьеры как для электронов, так и для дырок. Высота потенциаль ного барьера еjопределяется первоначальной разностью положений уровня Ферми в обоих полупроводниках. Все энергетические уровни акцепторного полупроводника подняты относительно уровней донорного полупроводника на высоту, равную еj, причем подъем происходит на толщине двойного слоя d.

Толщина d слоя p-n-перехода в полупроводниках составляет примерно

10^-б— 10^-7 м, а контактная разность потенциалов — десятые доли вольт. Носители тока способны преодолеть такую разность потенциалов лишь при температуре в несколько тысяч градусов, т. е. при обычных температурах равновесный контактный слой является запирающим (характеризуется повышенным сопротивлением).

Сопротивление запирающего слоя можно изменить с помощью внешнего электрического поля. Если приложенное к p-n-переходу внешнее электрическое поле направлено от n-полупроводника к p-полупроводнику (рис. 337, а), т. е. совпадает с полем контактного слоя, то оно вызывает движение электронов в n-полупроводнике и дырок в p-полупроводнике от границы р-n-перехода в противоположные стороны.

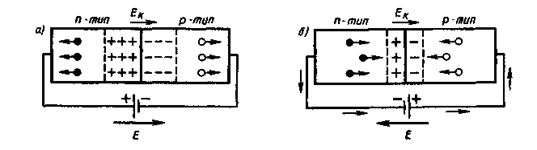
Рис. 337

В результате запирающий слой расширится и его сопротивление возрастет. Направление внешнего поля, расширяющего запирающий слой, называется запирающим (обратным). В этом направлении электрический ток через p-n-переход практически не проходит. Ток в запирающем слое в запирающем направлении образуется лишь за счет неосновных носителей тока (электронов в p-полупроводнике и дырок в n-полупроводнике).

Если приложенное к p-n-переходу внешнее электрическое поле направлено противоположно полю контактного слоя (рис. 337, 6), то оно вызывает движение электронов в n-полупроводнике и дырок в p-полупроводнике к границе p-n-перехода навстречу друг другу. В этой области они рекомбинируют, толщина контактного слоя и его сопротивление уменьшаются. Следовательно, в этом направлении электрический ток проходит сквозь p-n-переход в направлении от p-полупроводника к n-полупроводнику; оно называется пропускным (прямым).

Таким образом, p-n-переход обладает односторонней (вентильной) проводимостью.

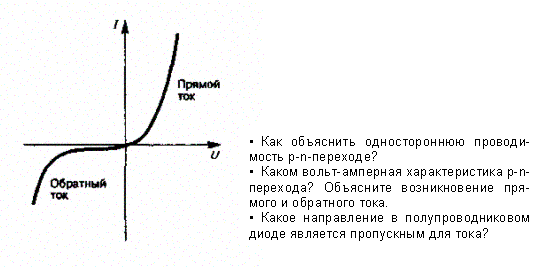
На рис. 338 представлена вольт-амперная характеристика p-n-перехода. Как уже указывалось, при пропускном (прямом) напряжении внешнее электрическое поле способствует движению основных носителей тока к границе p-n-перехода (см. рис. 337, б). В результате толщина контактного слоя уменьшается. Соответственно уменьшается и сопротивление перехода (тем сильнее, чем больше напряжение), а сила тока становится большой (правая ветвь на рис. 338). Это направление тока называется прямым.

.

* П. Бугер (1698—1758) — французский ученый.