
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормальный закон распределения.
|
|
Нормальный закон распределения имеет плотность распределения
 (*)
(*)
где m и s> 0 некоторые числовые параметры. В разделе «Предельные теоремы теории вероятностей.» будут обсуждены причины, в силу которых нормальный закон распределения играет важную
роль в теории вероятностей и ее приложениях.
х. Легко убедиться, что кривая, определяемая функцией распределения (*), имеет максимум в точке x=m, а точки перегиба отстоят от точки x=m на расстоянии s и при 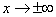 функция (*) асимптотически приближается к нулю. График функции (*) изображен на рис. 9
функция (*) асимптотически приближается к нулю. График функции (*) изображен на рис. 9
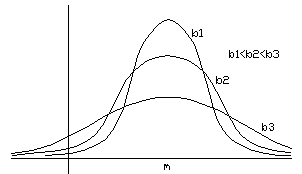
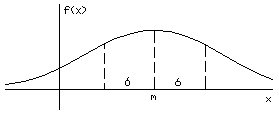
Рисунок 9
Рисунок 10.
В зависимости от величины параметров кривая плотности вероятности имеет различный вид и поэтому правильнее было бы говорить о семействе нормальных законов распределения (на рис. 10 показана зависимость формы кривой распределения от величины s при фиксированном m).
Выясним теперь вероятностный смысл параметров функции распределения. Для этого вычислим математическое ожидание и дисперсию случайной величины распределенной нормально.

Введем новую переменную
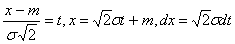
Тогда 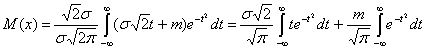
Первый интеграл равен нулю, так как под знаком интеграла стоит нечетная функция, а пределы интегрирования симметричны. Второй интеграл известен как интеграл Пуассона  .
.
Поэтому M(x)=m
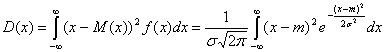
Если сделать ту же замену переменных и проделать необходимые преобразования, то можно убедиться, что
 .
.
Итак, параметры нормального закона распределения m и s равны соответственно математическому ожиданию и среднему квадратическому отклонению случайной величины распределенной по этому закону. Так как параметры однозначно определяют нормальный закон распределения, то для нормального закона часто используют обозначение 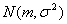 .
.
Получим две важные формулы для нахождения вероятности.
1)Пусть случайная величина имеет закон распределения 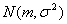 . Вычислим вероятность того, что она примет значение из интервала [a, b].
. Вычислим вероятность того, что она примет значение из интервала [a, b].
На основании свойств функции плотности вероятности можно записать
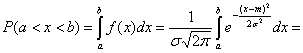
Сделаем замену переменных 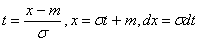
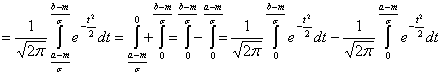
Введем в рассмотрение функцию (функцию Лапласа)
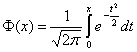
С помощью нее искомую вероятность можно записать
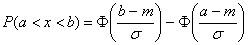 (**)
(**)
Интеграл 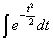 в явном виде не берется и значения функции Ф(х) были вычислены с помощью численных методом, а результаты сведены в таблицу. По таблице для каждого x можно найти соответствующее значение функции Ф(х). Функция Ф(х) нечетна, т.е
в явном виде не берется и значения функции Ф(х) были вычислены с помощью численных методом, а результаты сведены в таблицу. По таблице для каждого x можно найти соответствующее значение функции Ф(х). Функция Ф(х) нечетна, т.е 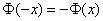 , и имеем график
, и имеем график
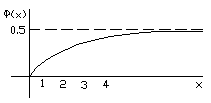
поэтому таблицы обычно приводятся только для положительных значений х и только из интервала 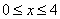 . При значениях х> 4 значения функции Ф(х) можно брать равным 0.5.
. При значениях х> 4 значения функции Ф(х) можно брать равным 0.5.
2)Для случайной величины, имеющей закон распределения 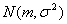 , найдем вероятность того, что отклонение этой случайной величины от своего математического ожидания не превысит величины a, т.е. вычислим вероятность
, найдем вероятность того, что отклонение этой случайной величины от своего математического ожидания не превысит величины a, т.е. вычислим вероятность

Неравенство под знаком вероятности эквивалентно неравенствам -a< x-m< a или 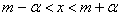 . Заменим в формуле (10) a через m-a, b – через m+a
. Заменим в формуле (10) a через m-a, b – через m+a
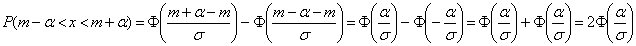 В результате получим формулу
В результате получим формулу
P( 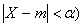 =2
=2 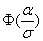 (***)
(***)
Замечание. Для случайной величины Х с математическим ожиданием М(х) и дисперсией D(x) случайная величина 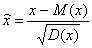 называется соответствующей нормированной случайной величиной. Нормированная случайная величина удобна тем, что
называется соответствующей нормированной случайной величиной. Нормированная случайная величина удобна тем, что  и
и 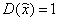 . В этом можно убедиться непосредственно
. В этом можно убедиться непосредственно
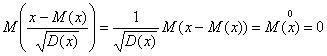
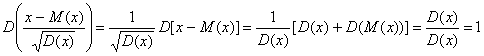
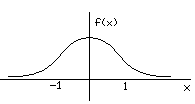 Геометрически нормировка означает, что начало координат переносится в точку с координатой М(х), а масштаб изменяется так, чтобы дисперсия
Геометрически нормировка означает, что начало координат переносится в точку с координатой М(х), а масштаб изменяется так, чтобы дисперсия 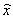 была равна единице. Если случайную величину х, имеющую закон распределения
была равна единице. Если случайную величину х, имеющую закон распределения 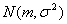 пронормировать, то случайная величина
пронормировать, то случайная величина 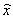 будет иметь закон распределения N(0, 1), определяемый функцией плотности вероятности
будет иметь закон распределения N(0, 1), определяемый функцией плотности вероятности
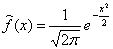
При выводе формулы (**) случайная величина Х нормировалась с помощью подстановки 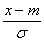 . Очевидно, что изменения масштаба не изменяет «вероятностный механизм явления», поэтому
. Очевидно, что изменения масштаба не изменяет «вероятностный механизм явления», поэтому
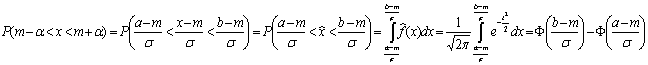
т.е. для вычисления вероятностей мы от любого закона распределения 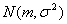 переходим к N(0, 1), а для закона N(0, 1) соответствующие вероятности заданы в виде таблиц функции Ф(х).
переходим к N(0, 1), а для закона N(0, 1) соответствующие вероятности заданы в виде таблиц функции Ф(х).
Двумерный нормальный закон распределения.. Систему случайных величин можно интерпретировать как случайную точку на плоскости. Нормальный закон распределения для системы (Х, У) называется двумерным нормальным законом распределения и имеет плотность вероятности
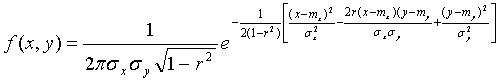
где 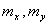 - математические ожидания соответственно случайных величин Х и У,
- математические ожидания соответственно случайных величин Х и У, 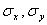 - средние квадратические отклонения этих величин, r – коэффициент корреляции Х и У. поверхность f(x, y) имеет вид
- средние квадратические отклонения этих величин, r – коэффициент корреляции Х и У. поверхность f(x, y) имеет вид
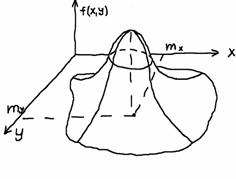
Двумерный нормальный закон распределения имеет, например, точка попадания снаряда из орудия, которое хорошо пристреляно по цели имеющей координаты 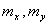 .
.
Если случайные величины независимы, то r=0 и функция плотности вероятности f(x, y) имеет вид
а 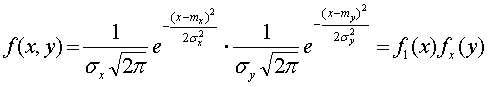 ,
,
что соответствует упомянутому нами свойству систем независимых случайных величин (7).
Используя формулу (6) и f(x, y) можно вычислить вероятность попадания ХУ в любую область плотности. Особенно просто это сделать, если Х и У независимы, а область представляет собой прямоугольник со сторонами параллельными осям координат.

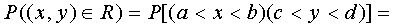

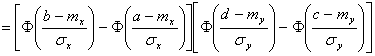
Можно ввести в рассмотрение нормальные законы распределения, имеющие большую размерность, например, трехмерные.
|