
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Отбор информативных признаков
|
|
Будем считать, что набор исходных признаков задан. Фактически его определяет учитель. Важно, чтобы в него вошли те признаки, которые действительно несут различительную информацию. Выполнение этого условия в решающей степени зависит от опыта и интуиции учителя, хорошего знания им той предметной области, для которой создаётся система распознавания. Если исходное признаковое пространство задано, то отбор меньшего числа наиболее информативных признаков (формирование признакового пространства меньшей размерности) поддаётся формализации. Пусть 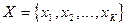 – исходное признаковое пространство,
– исходное признаковое пространство, 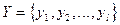 – преобразованное признаковое пространство,
– преобразованное признаковое пространство, 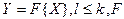 – некоторая функция.
– некоторая функция.
На рис. 16 представлено линейное преобразование координат
 .
.
После преобразования признак 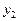 не несёт различительной информации и его использование для распознавания не имеет смысла.
не несёт различительной информации и его использование для распознавания не имеет смысла.
На рис. 17 проиллюстрирован переход от декартовой системы координат к полярной, что привело к целесообразности отбрасывания признака 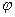 .
.
Такого рода преобразования приводят к упрощению решающих правил, т.к. их приходится строить в пространстве меньшей размерности. Однако при этом возникает необходимость в реализации преобразования 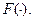 Поэтому суммарного упрощения может и не получиться, особенно при цифровой реализации преобразования признакового пространства. Хорошо, если датчики, измеряющие значения исходных признаков, по своей физической природе таковы, что попутно осуществляют требуемое преобразование.
Поэтому суммарного упрощения может и не получиться, особенно при цифровой реализации преобразования признакового пространства. Хорошо, если датчики, измеряющие значения исходных признаков, по своей физической природе таковы, что попутно осуществляют требуемое преобразование.





























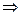




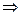
















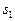

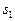

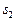
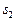


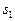
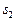




 |
| 



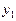
Рис. 16. Линейное преобразование координат
с последующим отбрасыванием одного из признаков
Особо выделим следующий тип линейного преобразования:
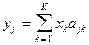 ,
,
где 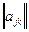 – диагональная матрица, причём её элементы равны либо 0, либо 1.
– диагональная матрица, причём её элементы равны либо 0, либо 1.
Это означает, что из исходной системы признаков часть отбрасывается. Разумеется, остающиеся признаки должны образовывать наиболее информативную подсистему. Таким образом, нужно разумно организовать процедуру отбора по одному из ранее рассмотренных критериев информативности. Рассмотрим некоторые подходы.
Оптимальное решение задачи даёт полный перебор. Если исходная система содержит  признаков, а нам нужно выбрать наилучшую подсистему, содержащую
признаков, а нам нужно выбрать наилучшую подсистему, содержащую 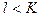 признаков, то придётся рассмотреть
признаков, то придётся рассмотреть 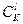 (число сочетаний из
(число сочетаний из  элементов по
элементов по 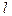 ) возможных в данном случае подсистем. Причём рассмотрение каждой подсистемы состоит в оценке значения критерия информативности, что само по себе является трудоёмкой задачей, особенно если в качестве критерия использовать относительное число ошибок распознавания. Для иллюстрации укажем, что для отбора из 20 исходных признаков пяти наиболее информативных приходится иметь дело примерно с 15, 5× 103 вариантами. Если же количество исходных признаков – сотни, то полный перебор становится неприемлемым. Переходят к разумным процедурам направленного отбора, которые в общем случае не гарантируют оптимального решения, но хотя бы обеспечивают не худший выбор.
) возможных в данном случае подсистем. Причём рассмотрение каждой подсистемы состоит в оценке значения критерия информативности, что само по себе является трудоёмкой задачей, особенно если в качестве критерия использовать относительное число ошибок распознавания. Для иллюстрации укажем, что для отбора из 20 исходных признаков пяти наиболее информативных приходится иметь дело примерно с 15, 5× 103 вариантами. Если же количество исходных признаков – сотни, то полный перебор становится неприемлемым. Переходят к разумным процедурам направленного отбора, которые в общем случае не гарантируют оптимального решения, но хотя бы обеспечивают не худший выбор.
 |
Рис. 17. Переход к полярной системе координат
с последующим отбрасыванием признака 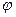
Рассмотрим некоторые из применяемых процедур.
1. Оценивается информативность каждого из исходных признаков, взятого в отдельности. Затем признаки ранжируются по убыванию информативности. После этого отбираются 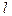 первых признаков. Здесь число рассматриваемых вариантов
первых признаков. Здесь число рассматриваемых вариантов 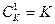 . При таком подходе оптимальность выбора гарантирована только в том случае, если все исходные признаки статистически не зависят друг от друга. В противном случае (а они чаще всего и встречаются на практике) решение может оказаться далеко не оптимальным.
. При таком подходе оптимальность выбора гарантирована только в том случае, если все исходные признаки статистически не зависят друг от друга. В противном случае (а они чаще всего и встречаются на практике) решение может оказаться далеко не оптимальным.
2. Предполагается, что признаки статистически зависимы. Сначала отбирается самый индивидуально информативный признак (просматривается  вариантов). Затем к первому отобранному признаку присоединяется ещё один из оставшихся, составляющий с первым самую информативную пару (просматривается
вариантов). Затем к первому отобранному признаку присоединяется ещё один из оставшихся, составляющий с первым самую информативную пару (просматривается 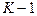 вариантов). После этого к отобранной паре присоединяется ещё один из оставшихся признаков, составляющий с ранее отобранной парой наиболее информативную тройку (просматривается
вариантов). После этого к отобранной паре присоединяется ещё один из оставшихся признаков, составляющий с ранее отобранной парой наиболее информативную тройку (просматривается 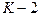 вариантов) и т.д. до получения совокупности из
вариантов) и т.д. до получения совокупности из 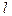 признаков. Здесь число просматриваемых вариантов составляет величину
признаков. Здесь число просматриваемых вариантов составляет величину 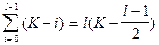 . Для иллюстрации отметим, что для отбора 5 признаков из 20 при данном подходе требуется просмотреть 90 вариантов, что примерно в 170 раз меньше, чем при полном переборе.
. Для иллюстрации отметим, что для отбора 5 признаков из 20 при данном подходе требуется просмотреть 90 вариантов, что примерно в 170 раз меньше, чем при полном переборе.
3. Последовательное отбрасывание признаков. Этот подход похож на предыдущий. Из совокупности, содержащей  признаков, отбрасывается тот, который даёт минимальное уменьшение информативности. Затем из оставшейся совокупности, содержащей
признаков, отбрасывается тот, который даёт минимальное уменьшение информативности. Затем из оставшейся совокупности, содержащей 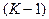 признаков, отбрасывается ещё один, минимально уменьшающий информативность, и т.д., пока не останется
признаков, отбрасывается ещё один, минимально уменьшающий информативность, и т.д., пока не останется 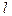 признаков. Из этих двух подходов (последовательное присоединение признаков и последовательное отбрасывание признаков) целесообразно использовать первый при
признаков. Из этих двух подходов (последовательное присоединение признаков и последовательное отбрасывание признаков) целесообразно использовать первый при  и второй при
и второй при 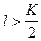 , если ориентироваться на число просматриваемых вариантов. Что касается результатов отбора, то он в общем случае может оказаться различным.
, если ориентироваться на число просматриваемых вариантов. Что касается результатов отбора, то он в общем случае может оказаться различным.
4. Случайный поиск. Случайным образом отбираются номера 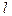 признаков и оценивается информативность этой подсистемы. Затем снова и независимо от предыдущего набора случайно формируется другая система из
признаков и оценивается информативность этой подсистемы. Затем снова и независимо от предыдущего набора случайно формируется другая система из 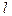 признаков. Так повторяется
признаков. Так повторяется 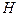 раз. Из
раз. Из 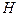 наборов признаков отбирается тот, который имеет наибольшую информативность. Чем
наборов признаков отбирается тот, который имеет наибольшую информативность. Чем 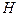 больше, тем выше вероятность выбора наилучшей подсистемы. При
больше, тем выше вероятность выбора наилучшей подсистемы. При 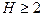 можно, по крайней мере, утверждать, что наш выбор не оказался наихудшим (если, конечно, выбранные подсистемы не оказались одинаковыми по информативности).
можно, по крайней мере, утверждать, что наш выбор не оказался наихудшим (если, конечно, выбранные подсистемы не оказались одинаковыми по информативности).
5. Случайный поиск с адаптацией. Это последовательная направленная процедура, основанная на случайном поиске с учётом результатов предыдущих отборов. В начале процедуры шансы всех исходных признаков на вхождение в подсистему, состоящую из 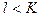 признаков, принимаются равными. Для случайного отбора используется датчик равномерно распределённых в интервале
признаков, принимаются равными. Для случайного отбора используется датчик равномерно распределённых в интервале 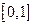 случайных (псевдослучайных) чисел. Этот интервал разбивается на
случайных (псевдослучайных) чисел. Этот интервал разбивается на  равных отрезков. Первый отрезок ставится в соответствие признаку
равных отрезков. Первый отрезок ставится в соответствие признаку 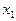 , второй –
, второй – 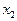 и т.д. Длина каждого отрезка равна вероятности
и т.д. Длина каждого отрезка равна вероятности 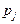 включения
включения 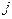 -го признака в информативную подсистему. Как уже отмечалось, сначала эти вероятности для всех признаков одинаковы. Датчиком случайных чисел выбирается
-го признака в информативную подсистему. Как уже отмечалось, сначала эти вероятности для всех признаков одинаковы. Датчиком случайных чисел выбирается 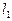 различных отрезков. Для тех
различных отрезков. Для тех 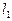 признаков из
признаков из  , которые соответствуют этим отрезкам, определяется значение критерия информативности
, которые соответствуют этим отрезкам, определяется значение критерия информативности 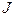 . После получения первой группы из
. После получения первой группы из 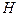 случайно выбранных подсистем определяется
случайно выбранных подсистем определяется 
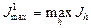 и
и 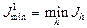 . Адаптация состоит в изменении вектора вероятностей
. Адаптация состоит в изменении вектора вероятностей 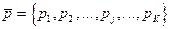 выбора признаков на последующих этапах поиска в зависимости от результатов предыдущих этапов: длина отрезка в интервале
выбора признаков на последующих этапах поиска в зависимости от результатов предыдущих этапов: длина отрезка в интервале 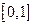 , соответствующая признаку, попавшему в самую плохую подсистему, уменьшается (признак " наказывается"), а попавшему в самую хорошую подсистему – увеличивается (признак " поощряется"). Длины отрезков изменяются на величину
, соответствующая признаку, попавшему в самую плохую подсистему, уменьшается (признак " наказывается"), а попавшему в самую хорошую подсистему – увеличивается (признак " поощряется"). Длины отрезков изменяются на величину 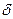
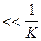 . После перебора ряда групп вероятность выбора признаков, часто встречающихся в удачных сочетаниях, становится существенно больше других, и датчик случайных чисел начинает выбирать одно и то же сочетание из
. После перебора ряда групп вероятность выбора признаков, часто встречающихся в удачных сочетаниях, становится существенно больше других, и датчик случайных чисел начинает выбирать одно и то же сочетание из 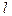 признаков. Чем больше
признаков. Чем больше 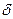 , тем быстрее сходимость процедуры, но тем ниже вероятность " выхода" на наилучшую подсистему. И наоборот, чем меньше
, тем быстрее сходимость процедуры, но тем ниже вероятность " выхода" на наилучшую подсистему. И наоборот, чем меньше 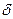 , тем медленнее сходимость, но выше вероятность выбора наилучшей подсистемы. Конкретный выбор значения
, тем медленнее сходимость, но выше вероятность выбора наилучшей подсистемы. Конкретный выбор значения 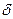 должен быть таким, чтобы процедура сходилась при общем числе выборов
должен быть таким, чтобы процедура сходилась при общем числе выборов 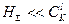 , а вероятность нахождения наилучшей подсистемы или близкой к ней по информативности была бы близка к единице.
, а вероятность нахождения наилучшей подсистемы или близкой к ней по информативности была бы близка к единице.
Список литературы
1. Айзерман А.А., Браверман Э.М., Розоноэр Э.И. Метод потенциальных функций в теории обучения машин. – М.: Наука, 1970.
2. Волошин Г.Я., Бурлаков И.А., Косенкова С.Т. Статистические методы решения задач распознавания, основанные на аппроксимационном подходе.
3. Горелик А.Л., Скрипкин В.А. Методы распознавания. – М.: Высш. шк., 1977.
4. Дуда Р., Харт П. Распознавание образов и анализ сцен. – М.: Мир, 1976.
5. Загоруйко Н.Г. Методы распознавания и их применение. – М.: Сов. радио, 1972.
6. Патрик Э. Основы теории распознавания образов. – М.: Сов. радио, 1980.
7. Фу К.С. Последовательные методы в распознавании образов и обучении машин. – М.: Наука, 1971.
8. Фу К.С. Структурные методы в распознавании образов. – М.: Мир, 1977.