
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Умозаключение как форма мышления
|
|
Категорические суждения
При рассмотрении способов образования сложных суждений из простых внутреннее строение простых суждений во внимание не принималось. Они брались как неразложимые атомы, обладающие только одним свойством: быть истинными или ложными. Простые суждения не случайно иногда именуются атомарными: из них, как из элементарных кирпичиков, с помощью логических связок «и», «или» и т.п. строятся разнообразные сложные, «молекулярные» суждения.
Теперь следует остановиться на вопросе о внутреннем строении, или внутренней структуре, самих простых суждений: из каких конкретных частей они слагаются, и как эти части связаны между собой.
Сразу же нужно подчеркнуть, что простые суждения могут разлагаться на составные части по-разному. Результат разложения зависит от цели, ради которой оно осуществляется, т.е. от той теории логического вывода, в рамках которой анализируются такие суждения.
Далее будет рассматриваться лишь одна разновидность простых суждений – категорические суждения.
Особый интерес к категорическим суждениям объясняется, прежде всего, тем, что с исследования их логических связей началось развитие логики как науки. Кроме того, суждения этого типа широко используются в наших рассуждениях.
Категорическое суждение – это суждение, в котором утверждается или отрицается наличие какого-то признака у всех или некоторых предметов рассматриваемого класса.
Примеры. В суждении «Все динозавры вымерли» всем динозаврам, или, что то же самое, каждому из динозавров, приписывается признак «быть вымершими». В суждении «Некоторые динозавры летали» способность летать приписывается некоторым динозаврам. В суждении «Все кометы не астероиды» отрицается наличие признака «быть астероидом» у каждой из комет. В суждении «Некоторые животные не являются травоядными» отрицается травоядность некоторых животных.
Если отвлечься от количественной характеристики, которая содержится в категорическом суждении и выражается словами «все» и «некоторые», то получатся два варианта таких суждений: утвердительный и отрицательный. Их структура:
«S есть Р» и «S не есть Р»,
где буква S представляет имя того предмета, о котором идет речь в суждении, а буква Р – имя признака, присущего или не присущего этому предмету.
Предмет, о котором говорится в категорическом суждении, называется субъектом, а его признак – предикатом.
Субъект и предикат именуются терминами категорического суждения и соединяются между собой связками «есть» или «не есть» ‒ «является» или «не является» и т.п.
Пример. В суждении «Солнце есть звезда» терминами являются имена «Солнце» и «звезда». Первый из них – субъект суждения, второй – его предикат, а слово «есть» – связка.
Простые суждения типа «S есть (не есть) Р» называются атрибутивными.
В них осуществляется атрибуция (приписывание) какого-то свойства предмету.
Атрибутивным суждениям противостоят суждения об отношениях, в которых устанавливаются отношения между двумя или большим числом предметов.
Примеры. «Три меньше пяти», «Киев больше Одессы», «Весна лучше осени», «Париж находится между Москвой и Нью-Йорком» и т.п.
В суждениях типа «Все S есть (не есть) Р» слово «все» означает «каждый из предметов соответствующего класса». В суждениях типа «Некоторые S есть (не есть) Р» слово «некоторые» употребляется в неисключающем смысле и означает «некоторые, а может быть все». В исключающем смысле слово «некоторые» означает «только некоторые», или «некоторые, но не все».
В категорических суждениях утверждается или отрицается принадлежность каких-то признаков рассматриваемым предметам и указывается, идет ли речь обо всех этих предметах или же о некоторых из них. Возможны, таким образом, четыре вида категорических суждений:
Все S есть Р – общеутвердительное суждение.
Некоторые S есть Р – частноутвердительное суждение.
Все S не есть Р – общеотрицательное суждение.
Некоторые S не есть Р – частноотрицательное суждение.
Категорические суждения можно рассматривать как результаты подстановки каких-то имен в следующие выражения с «многоточиями»:
«Все... есть...», «Некоторые... есть...», «Все... не есть...» и «Некоторые... не есть...». Каждое из этих выражений является логической постоянной, позволяющей из двух имен получить суждение.
Примеры. Подставляя вместо многоточий имена «летающие» и «птицы», получаем, соответственно, следующие суждения: «Все летающие есть птицы», «Некоторые летающие есть птицы», «Все летающие не есть птицы» и «Некоторые летающие не есть птицы». Первое и третье суждения являются ложными, а второе и четвертое – истинными.
В традиционной логике предполагается также, что имена, подставляемые вместо многоточий, не должны быть единичными или пустыми.
Примеры. Суждения типа «Платон – человек», «Все золотые горы – это горы» не относятся к категорическим в традиционном смысле, поскольку «Платон» – единичное имя, а «золотые горы» – пустое имя.
Введем обозначения:
«Все... есть...» ‒ а(первая гласная латинского слова affirmo – утверждаю).
«Некоторые... есть...» ‒ i (вторая гласная латинского слова affirmo).
«Все... не есть...» ‒ е (первая гласная латинского слова nego – отрицаю).
«Некоторые... не есть...» ‒ о (вторая гласная латинского слова nego).
SaP – «Все S есть Р» – «Все жидкости упруги»,
SiP – «Некоторые S есть Р» – «Некоторые животные говорят»,
SeP – «Все S не есть Р» – «Все дельфины не есть рыбы»,
SoP – «Некоторые S не есть Р» – «Некоторые металлы не есть жидкости».
Отношения между терминами в четырех видах категорических суждений представляются с помощью кругов Эйлера следующим образом:

Логический квадрат
Некоторые отношения между четырьмя видами категорических суждений графически представляются так называемым логическим квадратом.

В отношении противоречия (контрадикторности) находятсясуждения SaP и SoP, SeP и SiP. Они не могут быть одновременно истинными и ложными. Если одно из них истинно, то другое ‒ ложно.
Примеры. Если суждение «Все киты дышат легкими» истинно, то суждение «Некоторые киты не дышат легкими» ложно. Если суждение «Некоторые медведи – не бурые» истинно, то суждение «Все медведи – бурые» ложно.
В отношении п ротивоположности (контрарности) находятся суждения SaP и SeP. Они могут вместе быть ложными, но не могут быть вместе истинными. Если одно из противоположных суждений истинно, то другое ложно.
Примеры. Суждения «Все спортсмены – гроссмейстеры» и «Ни один спортсмен не гроссмейстер» оба ложны. Поскольку суждение «У всех людей есть головы» истинно, то суждение «Ни у одного человека нет головы» ложно. Если суждение «Все металлы не являются газами» истинно, то суждение «Все металлы – газы» ложно.
В отношении частичного совпадения (субконтрарности) могут находиться суждения SiP и SoP. Они не могут быть одновременно ложными, но могут быть одновременно истинными.
Примеры. Если суждение «Некоторые овцы – хищники» ложно, то суждение «(По меньшей мере) некоторые овцы не являются хищниками» истинно. суждения же «Некоторые спортсмены – футболисты» и «Некоторые спортсмены не футболисты» оба истинны.
В отношении подчинения находятся попарно суждения SaP и SiP, SeP и SoP. Из подчиняющего суждения логически следует подчиненное: из SaP вытекает SiP и из SeP вытекает SoP. Это означает, что из истинности подчиняющего суждения логически следует истинность подчиненного, и из ложности подчиненного следует ложность подчиняющего.
Примеры. Из суждения «Все киты являются млекопитающими» следует суждение «Некоторые киты млекопитающие», а из суждения «Все металлы не являются сжимаемыми» следует суждение «Некоторые металлы не сжимаемы».
Категорический силлогизм
Категорический силлогизм (или просто: силлогизм) – это дедуктивное умозаключение, в котором из двух категорических суждений выводится новое категорическое суждение.
Логическая теория такого рода умозаключений называется силлогистикой. Она была создана Аристотелем.
В силлогистике выражения «Все... есть...», «Некоторые... есть...», «Все... не есть...» и «Некоторые... не есть...» рассматриваются как логические постоянные, т.е. берутся как единое целое. Это не суждения, а определенные логические формы, из которых получаются суждения путем подстановки вместо многоточий каких-то имен. Подставляемые имена называются терминами силлогизма.
Существенным является следующее традиционное ограничение: термины силлогизма не должны быть пустыми или отрицательными.
Пример силлогизма.
Все жидкости упруги.
Вода – жидкость.
Вода упруга.
В каждом силлогизме должно быть три термина: меньший, бó льший и средний.
Меньшим термином называется субъект заключения.
В примере таковым является термин «вода».
Бó льшим термином именуется предикат заключения.
В примере таким термином является термин «упруга».
Термин, присутствующий в посылках, но отсутствующий в заключении, называется средним.
В примере таким термином является термин «жидкость».
Меньший термин обозначается обычно буквой S, бó льший – буквой Р и средний – буквой М.
Посылка, в которую входит бó льший термин, называется бó льшей. Посылка с меньшим термином называется меньшей.
Большая посылка записывается первой, меньшая – второй.
Итак, в силлогизм входят три термина:
· S ‒ меньший термин: субъект заключения (входит также в меньшую посылку);
· P ‒ больший термин: предикат заключения (входит также в большую посылку);
· M ‒ средний термин: входит в обе посылки, но не входит в заключение.
Логическая форма приведенного силлогизма такова:
Все М есть Р.
Все S есть М.
Все S есть Р.
В силлогизме, как и во всяком дедуктивном умозаключении, в заключении не может содержаться информация, отсутствующая в посылках. Заключение только развертывает информацию посылок, но не может привносить новую информацию, отсутствующую в них.
В зависимости от положения среднего термина в посылках (является он субъектом или предикатом в большей и меньшей посылках) различаются четыре фигуры силлогизма.
1-я фигура 2-я фигура 3-я фигура 4-я фигура
Бо́ льшая посылка: M—P P—M M—P P—M
Меньшая посылка: S—M S—M M—S M—S
Заключение: S—P S—P S—P S—P
Схематически фигуры изображаются так:
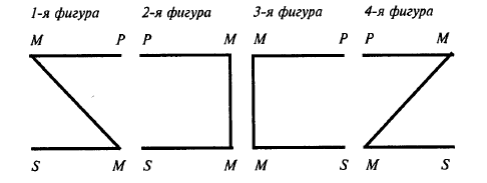
По схеме первой фигуры построен силлогизм:
Все птицы (М) имеют крылья (Р).
Все страусы (S) – птицы (М).
Все страусы имеют крылья.
По схеме второй фигуры построен силлогизм:
Все рыбы (Р) дышат жабрами (М).
Киты (S) не дышат жабрами (М).
Все киты не рыбы.
По схеме третьей фигуры построен силлогизм:
Все бамбуки (М) цветут один раз в жизни (Р).
Все бамбуки (М) – многолетние растения (S).
Некоторые многолетние растения цветут один раз в жизни.
По схеме четвертой фигуры построен силлогизм:
Все рыбы (Р) плавают (М).
Все плавающие (М) живут в воде (S).
Некоторые живущие в воде – рыбы.
Посылками и заключениями силлогизмов могут быть категорические суждения четырех видов: SaP, SiP, SeP и SoP.
Модусами силлогизма называются разновидности фигур, отличающиеся характером посылок и заключения.
Всего, с точки зрения всевозможных сочетаний посылок и заключения, в каждой фигуре насчитывается 64 модуса. В четырех фигурах 4 × 64 = 256 модусов.
Силлогизмы, как и все дедуктивные умозаключения, делятся на правильные и неправильные. Задача логической теории силлогизма – систематизировать правильные силлогизмы, указать их отличительные черты.
Из всех возможных модусов силлогизма только 19 модусов являются правильными.
Модусы изучались еще средневековыми школами логики, и для правильных модусов каждой фигуры были придуманы мнемонические имена.
Первую фигуру силлогизма Аристотель считал основной или совершенной. В XIII столетии для запоминания всех девятнадцати модусов и для приведения их к первой фигуре были составлены мнемонические стихи. Их первая строчка перечисляет модусы основной фигуры.
Bаrbara, Celarent, Darii, Ferioque prioris;
Cesare, Camestres, Festino, Baroko, sekundae;
Tertia, Darapti, Disamis, Datisi. Felapton,
Bоcardо, Ferison habet; quarta insuper addit.
Bramantip, Camenes, Dimaris, Fesapo, Fresison.
В каждом из этих названий содержатся три гласных буквы. Они указывают, какие именно категорические высказывания используются в модусе в качестве его посылок и заключения.
В приведенных стихах начальные буквы названных модусов указывают на тот модус первой фигуры, к которому надо привести данный модус. Так, Felapton приводится к Ferio, Disamis ‒ к Darii.
Пример. Название Celarent означает, что в этом модусе первой фигуры большей посылкой является общеотрицательное высказывание (SeP), меньшей – общеутвердительное (SaP) и заключением – общеотрицательное высказывание (SeP).
Каждой фигуре силлогизма соответствуют определенные модусы.
| 1-я фигура | 2-я фигура | 3-я фигура | 4-я фигура | |||
| Barbara | Cesare | Darapti | Bramantip | |||
| Celarent | Camestres | Disamis | Camenes | |||
| Darii | Festino | Datisi | Dimaris | |||
| Ferio | Baroco | Felapton | Fesapo | |||
| Bocardo | Fresison | |||||
| Ferison |
Для оценки правильности силлогизма могут использоваться круги Эйлера, иллюстрирующие отношения между объемами имен.
Пример. Возьмем силлогизм:
Все металлы (М) ковки (Р).
Железо (S) – металл (М).
Железо (S) ковко (Р).
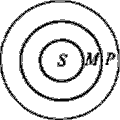
Отношения между тремя терминами этого силлогизма (модус Barbara) представляются тремя концентрическими кругами. Эта схема интерпретируется так: если все М (металлы) входят в объем Р (ковких тел), то с необходимостью S (железо) войдет в объем Р (ковких тел), что и утверждается в заключении «Железо ковко».
Пример.
Все рыбы (Р) не имеют перьев (М).
У всех птиц (S) есть перья (М).
Ни одна птица (S) не является рыбой (Р).
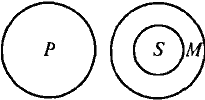
Отношения между терминами данного силлогизма (модус Cesare) представлены на рисунке. Он истолковывается так: если все S (птицы) входят в объем М (имеющие перья), а М не имеет ничего общего с Р (рыбы), то у S (птицы) нет ничего общего с Р (рыбы), что и утверждается в заключении.