
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пространственная и временная когерентность
|
|
Когерентность – это согласованное протекание двух или более волновых процессов.
Временная когерентность – когерентность колебаний, которые совершаются в одной и той же точке пространства в разные моменты времени и связана с разбросом волнового вектора по величине.
Монохроматическая световая волна представляет собой некоторую абстракцию. Всякая реальная волна представляет собой суперпозицию электромагнитных волн, частота которых заключена в некотором частотном интервале  . Кроме этого амплитуда и фаза колебаний в волне претерпевают непрерывные хаотические изменения во времени.
. Кроме этого амплитуда и фаза колебаний в волне претерпевают непрерывные хаотические изменения во времени.
Немонохроматичность света ведет сначала к ухудшению контрастности (видимости) интерференционных полос, а затем к полному исчезновению их по мере удаления ее от середины в опыте Юнга.
Монохроматическая волна:
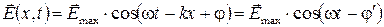
Реальная волна:

Изменение во времени обусловлено тем, что реальная световая волна образуется путём наложения цугов волн, испускаемых отдельными атомами, причём амплитуда, фаза и частота цугов волн отдельных атомов в общем случае не одинаковы. Для когерентности пучков необходимо, чтобы разность хода между ними не превосходила длину цуга. В противоположном случае будет происходить наложение независимых цугов волн, испущенных в разные моменты времени, и интерференция не возникает. Цуг – это последовательность “горбов” и “впадин” электромагнитного излучения, испускаемого атомом в возбужденном состоянии. Если время нахождения атома в возбуждённом состоянии  , то длина цуга
, то длина цуга  , где
, где 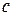 – скорость электромагнитной волны.
– скорость электромагнитной волны.
Реальную электромагнитную волну можно представить в виде
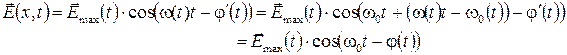 ,
,
где  – средняя частота. Таким образом, все случайные изменения частоты заносятся в фазу.
– средняя частота. Таким образом, все случайные изменения частоты заносятся в фазу.
Пусть в некоторой точке пространства складываются два однонаправленных колебания, создаваемых реальными световыми волнами. Для простоты будем считать, что амплитуда этих волн не зависит от времени

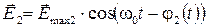
Результирующее колебание в точке наблюдения

Обе части уравнения возводим в квадрат:
 .
.
Последнее уравнение усредняем по периоду колебания:

Учитывая, что  , получаем, что интенсивность света в точке наблюдения
, получаем, что интенсивность света в точке наблюдения
 (12)
(12)
где  – разность фаз колебаний, создаваемых реальными волнами в точке наблюдения.
– разность фаз колебаний, создаваемых реальными волнами в точке наблюдения.
Если  за время наблюдения пробегает значения от -1 до 1, тогда
за время наблюдения пробегает значения от -1 до 1, тогда 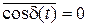 и в этом случае интерференция не наблюдается.
и в этом случае интерференция не наблюдается.
Если  за время наблюдения не успел измениться, то
за время наблюдения не успел измениться, то  и в этой точке мы можем наблюдать либо максимум, либо минимум интенсивности.
и в этой точке мы можем наблюдать либо максимум, либо минимум интенсивности.
Т.о. наличие интерференционной картины, создаваемой реальными волнами, зависит от времени наблюдения, и одним прибором мы можем регистрировать интерференционную картину, а другим прибором – нет.
С течением времени интенсивность в точке наблюдения постоянно меняется (то минимум, то максимум), и результирующая интенсивность определяется ее средним значением за время наблюдения (время срабатывания прибора: фотоаппарат  , а глаз человека
, а глаз человека  ).
).
Время когерентности 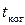 – время, за которое фаза результирующего колебания
– время, за которое фаза результирующего колебания  изменяется на
изменяется на  (
( изменяется от 1 до -1).
изменяется от 1 до -1).
Если время срабатывания прибора больше времени когерентности 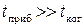 , то интерференционная картина не наблюдается, если время срабатывания прибора меньше времени когерентности
, то интерференционная картина не наблюдается, если время срабатывания прибора меньше времени когерентности  , то – наблюдается.
, то – наблюдается.
Расстояние, которое проходит волна за время когерентности, называется длиной когерентности:
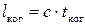 .
.
Пусть имеется реальная гармоническая волна, интервал частот которой лежит в диапазоне 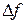 . Из частотного анализа доказывается, что время когерентности обратно пропорционально ширине частотного интервала:
. Из частотного анализа доказывается, что время когерентности обратно пропорционально ширине частотного интервала:
 .
.
Из определения длины волны  следует
следует

Дифференцируем последнее выражение

Тогда время когерентности будет определяться
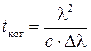 (13)
(13)
а длина когерентности:
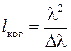 . (14)
. (14)
Чем шире интервал частот, тем время когерентности меньше. Если  (
( ), то получается волна является монохроматической и
), то получается волна является монохроматической и 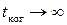 (
( ).
).
Если оптическая разность хода между двумя реальными волнами меньше длины когерентности, то интерференционная картина наблюдается. Если оптическая разность хода между двумя реальными волнами больше длины когерентности, то интерференционная картина не наблюдается. Физически это означает, что если оптическая разность хода интерферирующих волн становится больше длины когерентности, то в данной точке интерферирующего поля складываются колебания, испущенные атомом в моменты времени, отличающиеся более чем на время когерентности.
Временная когерентность накладывает условие на число видимых полос интерференционной картины:


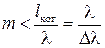 . (15)
. (15)
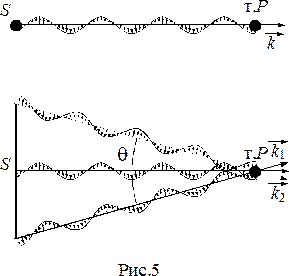 Пространственная когерентность – это когерентность колебаний, которые совершаются в один и тот же момент времени в различных точках пространства и связана с разбросом волнового вектора по направлению
Пространственная когерентность – это когерентность колебаний, которые совершаются в один и тот же момент времени в различных точках пространства и связана с разбросом волнового вектора по направлению
Пусть имеется точечный монохроматический источник света. Т.к. источник точечный, то волновой вектор в т. P будет иметь одно направление.
Рассмотрим протяжённый источник, все участки которого излучают волны (рис.5). Из рисунка видно, что в точке наблюдения вектор  имеет различные направления, т.е. наблюдается разброс волнового вектора по направлениям. Угол
имеет различные направления, т.е. наблюдается разброс волнового вектора по направлениям. Угол 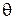 называется угловым размером источника.
называется угловым размером источника.
Рассмотрим изложенный ранее опыт Юнга, где в качестве источника монохроматического излучения берется протяжённый источник (через  обозначим линейный размер источника), все участки которого излучают световые волны (рис.6). На пути света стави
обозначим линейный размер источника), все участки которого излучают световые волны (рис.6). На пути света стави  м двухщелевую диафрагму, расстояние между щелями которой обозначим через
м двухщелевую диафрагму, расстояние между щелями которой обозначим через 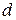 , и экран наблюдения. Предполагается, что не только расстояние
, и экран наблюдения. Предполагается, что не только расстояние 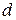 , но также размеры щелей экрана малы по сравнению с расстоянием
, но также размеры щелей экрана малы по сравнению с расстоянием 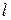 . Интерференционную картину на экране можно представить как наложение интерференционных картин от точечных источников, на которые мысленно разобьем
. Интерференционную картину на экране можно представить как наложение интерференционных картин от точечных источников, на которые мысленно разобьем  . Т. о. интенсивность света на экране будет представлять собой суперпозицию интенсивностей, создаваемых отдельными участками источника.
. Т. о. интенсивность света на экране будет представлять собой суперпозицию интенсивностей, создаваемых отдельными участками источника.

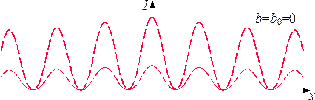

 Пусть положение максимумов на экране наблюдения от точечного источника, взятого посередине источника
Пусть положение максимумов на экране наблюдения от точечного источника, взятого посередине источника  – точка 1 – таково, как отмечено сплошными линиями на рис.6. Максимумы от источника, взятого около верхнего края
– точка 1 – таково, как отмечено сплошными линиями на рис.6. Максимумы от источника, взятого около верхнего края  – точка 2 – будут смещены вниз, и отмечены штрихпунктирными линиями на этом же рисунке. Максимумы от источника, взятого около нижнего края
– точка 2 – будут смещены вниз, и отмечены штрихпунктирными линиями на этом же рисунке. Максимумы от источника, взятого около нижнего края  – точка 3 – будут смещены вверх, и отмечены пунктирными линиями на том же рисунке. Интервалы между максимумами заполнены максимумами от промежуточных точечных источников, расположенных между краями 2 и 3. При увеличении размеров источника
– точка 3 – будут смещены вверх, и отмечены пунктирными линиями на том же рисунке. Интервалы между максимумами заполнены максимумами от промежуточных точечных источников, расположенных между краями 2 и 3. При увеличении размеров источника  расстояния между максимумами от ее крайних элементов будут увеличиваться, т.е. интервалы между соседними максимумами от одного края будут постепенно заполняться максимумами от остальных элементов реального источника. То есть интерференционная картина постепенно размывается и при некоторой ширине щели практически исчезает.
расстояния между максимумами от ее крайних элементов будут увеличиваться, т.е. интервалы между соседними максимумами от одного края будут постепенно заполняться максимумами от остальных элементов реального источника. То есть интерференционная картина постепенно размывается и при некоторой ширине щели практически исчезает.

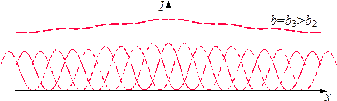 В последнем случае значение максимумов результирующего колебания мало отличаются от минимумов, и интерференционная картина на экране не наблюдается.
В последнем случае значение максимумов результирующего колебания мало отличаются от минимумов, и интерференционная картина на экране не наблюдается.
Это наблюдаемое явление можно объяснить и иначе, а именно: интерференционная картина исчезает вследствие того, что вторичные источники – щели  и
и  становятся некогерентными. Это позволяет нам говорить о ширине когерентности падающей на щели
становятся некогерентными. Это позволяет нам говорить о ширине когерентности падающей на щели  и
и  световой волны –
световой волны –  , на которой отдельные участки волны в достаточной степени когерентны между собой. Таким образом
, на которой отдельные участки волны в достаточной степени когерентны между собой. Таким образом  – характерное для данной установки расстояние между точками поверхности, перпендикулярной направлению распространения волны.
– характерное для данной установки расстояние между точками поверхности, перпендикулярной направлению распространения волны.
В рассматриваемой схеме опыта Юнга условие, при котором щели  и
и  становятся некогерентными источниками:
становятся некогерентными источниками:  , где
, где 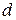 – расстояние между щелями. Интерференционная картина исчезает, когда ширина щели
– расстояние между щелями. Интерференционная картина исчезает, когда ширина щели 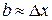 , где
, где  – ширина интерференционной полосы.
– ширина интерференционной полосы.
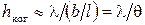 (16)
(16)
То есть ширина когерентности пропорциональна длине света и обратно пропорциональна угловой ширине источника относительно интересующего нас места (в опыте Юнга – относительно места расположения двух щелей).