Способы практической реализации интерференции

Метод, основанный на зеркалах Френеля

В 1816г. Френель осуществил 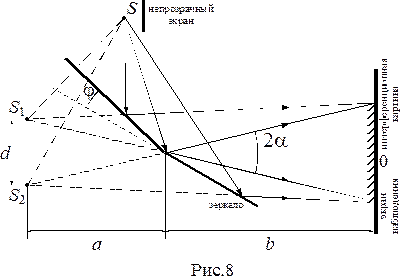следующий интерференционный опыт (рис.13). Свет от тонкой щели расходящимся пучком падает на систему двух зеркал, расположенных друг относительно друга под углом, близким к . Источник – узкая ярко освещенная щель 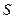, параллельная линии пересечения зеркал. Прямой свет от источника 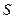загораживается непрозрачным экраном. Отраженные от зеркал пучки падают на экран и там, где они перекрываются (зона интерференции), возникает интерференционная картина в виде полос, параллельных щели . Отраженные от зеркал волны распространяются так, как если бы они распространялись из мнимых источников и , являющихся изображениями щели , а значит и можем считать когерентными, т.к. они образованы от одного источника.

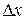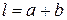Найдем ширину интерференционных полос на экране. Зная что . В данном случае и 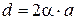, поэтому

.

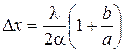Видно, что ширина полос растет с увеличением расстояния . Если же на бизеркала падает плоская волна, т. е. 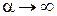, то

,

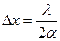и ширина полос в этом случае не зависит от расстояния – положения экрана.

Число возможных полос на экран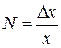е , где 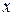– ширина зоны интерференции на экране, 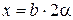. Следовательно,

.

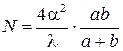Ширина щели должна быть: 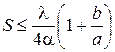, а степень монохроматичности используемого света .

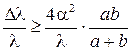Метод получения интерференции на основе зеркал Ллойда

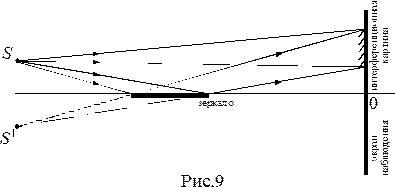Свет, исходит из точечного источника 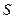, отражается от полированной плоской поверхности зеркала, установленного перпендикулярно экрану. В этой схеме (рис.9) интерферируют световая волна, исходящая из источника и волна, отраженная от зеркала. И на экране, в зоне перекрытия прямого и отраженного света наблюдаются полосы интерференции.

Кольца Ньютона

Кольца Ньютона – это кольцевые полосы равной толщины, наблюдаемые при отражении света от поверхностей зазора между плоской стеклянной пластинкой и плосковыпуклой линзой с большим радиусом кривизны (рис.16). В данном случае роль диэлектрического слоя переменной толщины, от поверхностей которого отражаются волны, играет воздушный зазор между пластинкой и линзой. Волна, отраженная от верхней поверхности линзы, в силу небольшой длины когерентности обычных источников света, некогерентна с волнами, отраженными от поверхностей зазора, и участия в образовании интерференционной картины не принимает.

Пусть свет с длиной волны 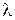нормально падает на систему линза-пластинка. Т.к. радиус кривизны линзы большой, а падение нормальное, то отражённый луч будет распределяться практически в обратном направлении.

Тогда оптическая разность хода между лучами 1 и 2

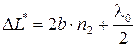, (17)

где – показатель преломления среды, заполняющий пространство между пластинкой и линзой.

Луч 2, при отражении от оптически более плотной среды 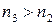, приобретает дополнительный набег фазы 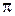, что соответствует дополнительной разности хода 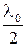. В зависимости от оптической разности хода лучи 1 и 2 будут складываться либо в фазе, либо в противофазе. В результате будем наблюдать картину кольцевых полос равной толщины (рис.17).

Из геометрии задачи (из прямоугольного треугольника ОАВ)

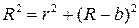
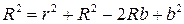
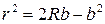
Т.к. линза имеет большой радиус кривизны, то есть 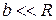, получим, что:

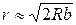. (18)

Если среда заполняющая пространство между линзой и пластинкой воздух (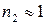) оптическая разность хода между лучами 1 и 2:

.

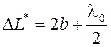а) Условие максимума. Светлые кольца возникают там, где оптическая разность хода волн, отраженных от обеих поверхностей зазора, равна четному числу полуволн:

, , .

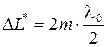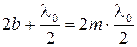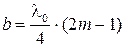Из последнего, уравнения и (18) следует, что радиус светлых колец Ньютона, соответствующих максимуму интерференции

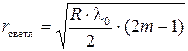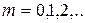, (19)

б) Условие минимума.Темные кольца возникают там, где оптическая разность хода волн, отраженных от обеих поверхностей зазора, равна нечетному числу полуволн:

, , .

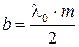Из последнего, уравнения и (18) следует, что радиус тёмных колец Ньютона, соответствующих минимуму интерференции

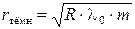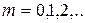, (20)

Эти формулы справедливы лишь для случая идеального (точечного) контакта сферической линзы с пластинкой. Но идеальных контактов не бывает, номера колец не равны вообще говоря порядку интерференции 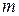, и это обстоятельство необходимо учитывать при расчетах.

Если в установке Ньютона линзу перемещать вверх параллельно самой себе, то из-за увеличения толщины воздушной прослойки каждая окружность постоянной (фиксированной) разности хода будет стягиваться к центру картины. Интерференционные кольца также будут стягиваться к центру, так как вдоль каждого кольца оптическая разность хода остается постоянной. Достигнув центра, каждое кольцо превратится в кружок, исчезающий при дальнейшем перемещении линзы. Таким образом, центр картины будет становиться попеременно то светлым, то темным. Одновременно на периферии поля зрения будут зарождаться и перемещаться к центру новые интерференционные кольца, пока каждое из них не исчезнет в центре картины. Можно сказать, что при перемещении линзы непрерывно вверх пропадают кольца самых низких порядков интерференции и зарождаются кольца более высоких порядков. Таким путем удается наблюдать интерференцию все более высокого порядка. Понятно, что для этого требуется свет высокой степени монохроматичности.

Если свет используемый в установке немонохроматичный, то при перемещении линзы вверх параллельно самой себе, радиусы колец более высоких порядков с некоторого момента появляться не будут. Это связано с тем что при некоторой толщине воздушной прослойки для немонохроматического света перестает выполняется условие временной и пространственной когерентности.

Интерференция в тонких пленках (пластинах)

Рассмотрим параллельный пучок монохроматического света падающего под углом 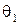на поверхность плоскопараллельной пластинки (пленки) с оптическим показателем преломления . Произвольно выбранный луч 1 падая на поверхность пластинки (т. А), частично отражается, частично преломляется (под углом 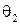) в пластинку. Преломленный луч доходит до нижней поверхности пластинки и отражается от нее (т. В). Отраженный луч идет в обратном направлении и достигнув верхней поверхности пластинки преломляется (т. С) и выходит из нее под углом 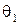в виде луча 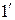. Падающий на пластинку в т. С под углом 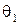луч 2 также отражается от нее в виде луча 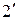, идущего совместно с лучом 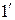. Вкладом лучей многократно отразившихся от пластины пренебрегаем.

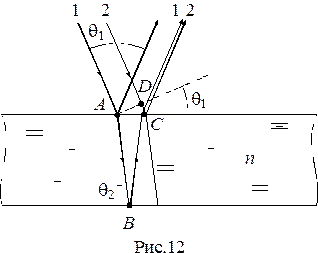В зависимости от разности хода лучей 1- 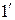и 2- 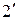они будут либо усиливать, либо гасить друг друга. Оптическая разность хода между лучами 1- 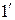и 2-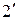

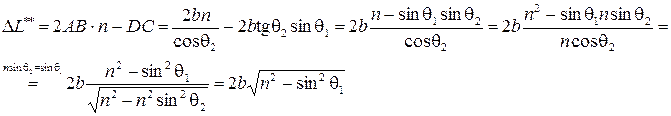Учитывая, что луч 2 отражается от среды оптически более плотной, и в момент отражения меняет скачком фазу на 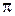(что соответствует разности хода 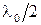), оптическая разность хода между лучами 1- 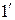и 2-

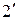
. (21)

Таким образом, разность хода между лучами зависит от ширины пластины, ее показателя преломления и от угла падения излучения .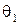

Если оптическая разность хода удовлетворяет условию максимума 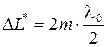, то луч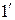и и 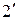будут складываться в фазе и усиливать друг друга. При этом все падающее на пластину излучение отразится от нее.

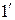Если оптическая разность хода удовлетворяет условию минимума , то лучи и 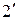будут складываться в противофазе и гасить друг друга. При этом все падающее на пластину пройдет через, нее не отражаясь.

Для наблюдения интерференции в пластинах необходимо выполнение условий временной и пространственной когерентности.

Согласно условию временной когерентности, интерференция наблюдается, если 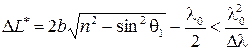. Отсюда следует, что интерференция наблюдается в пленках толщина которых 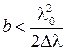. Здесь учтено , а .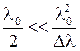

Согласно условию пространственной когерентности, интерференция наблюдается, если 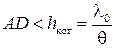, где 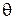– угловой размер источника.