Критерий положительной определённости квадратичной формы

1. " Необходимо." Имеется положительно определённая квадратичная форма. j-ый диагональный элемент положителен, так как k(x)> 0 в том числе и для вектора со всеми нулевыми координатами, кроме j-ой. При приведении матрицы к каноническому виду не будет нужно переставлять строки, и знаки главных миноров матрицы не изменятся. А в каноническом виде диагональные элементы положительны, и миноры положительны; следовательно, (так как их знак не менялся при преобразованиях), у положительно определённой квадратичной формы в любом базисе главные миноры матрицы положительны.

2. " Достаточно." Имеется положительность миноров. Первый минор определяет знак первого диагонального элемента в каноническом виде. Знак отношения M_i+1/M_i определяет знак i+1-ого элемента в диагональном виде. Так получим, что в каноническом виде все элементы на диагонали положительные, то есть квадратичная форма определена положительно.

Квадратичная функция 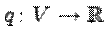над полем вещественных чисел 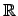называется положительно определенной, если 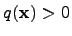для любого ненулевого вектора .

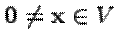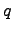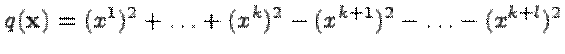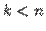Замечание. Если мы привели форму к нормальному виду , то для ее положительности надо чтобы . Если и , то форма будет неотрицательно определенной (на векторе 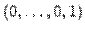значение формы 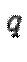равно нулю).

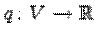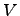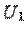Лемма. Пусть -- вещественная квадратичная функция на , а и 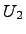-- подпространства в 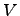такие, что 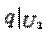-- положительно определенная квадратичная функция на 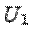, 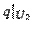-- неположительно определенная квадратичная функция на 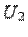, т.е. 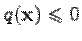для любого вектора 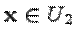. Тогда .

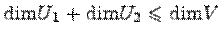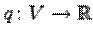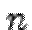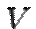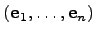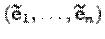Теорема. [Закон инерции] Если квадратичная функция на -мерном вещественном пространстве в базисе имеет нормальный вид , а в базисе имеет нормальный вид 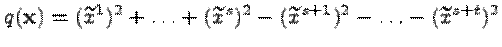, то и , причем .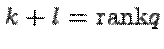

Определение. Число 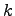называется положительным индексом инерции квадратичной функции 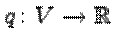. Число 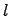называется отрицательным индексом инерции квадратичной функции 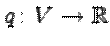. Пара 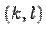или разность 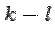называются сигнатурой квадратичной функции .

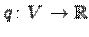Теорема. [Критерий Сильвестра] Пусть 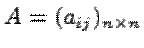-- матрица квадратичной функции 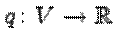в базисе 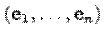вещественного 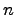-мерного пространства 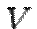. Квадратичная функция 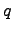является положительно определенной тогда и только тогда, когда все угловые миноры матрицы 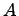положительны, т.е. , , где