Подведение учеников к формулировке определения понятия

Учитель на доске изображает 5 графиков и предлагает классу посмотреть на доску.

Как вы считаете, какие из функций являются возрастающими? Зарисуйте графики этих функций в тетради.

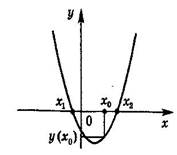
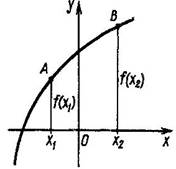
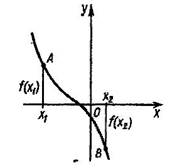
Рис. 7 Рис. 8 Рис. 9

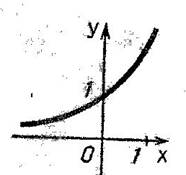
Рис. 10 Рис. 11

Начинается анализ каждого из графиков, изображенных на доске. Ученики высказывают свое мнение и пытаются его обосновать. Позже, учитель говорит правильный ответ. Возрастающие функции изображены на рисунках 8, 10. На рисунках 7 и 11 функции возрастают не на все области определения, а на промежутках.

II. Этап усвоения

Формулировка определения, овладение его содержанием

Возрастающая функция- это функция, у которой для любых двух значений аргумента из некоторого промежутка большему значению аргумента соответствует большее значение функции.

Запишем данное определение понятия в знаково-символьной форме.

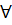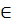Функция f(x) называется возрастающей на промежутке X, если х₁ X, х₂ 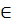X: х₁ < х₂, выполняется неравенство f(x₁) < f(х₂).

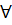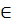х₁ X, х₂ 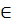X: х₁ < х₂,

в. н. f(x₁) < f(х₂).

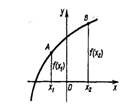
Рис. 12

Термин «функция» впервые встречается в письме немецкого математика Лейбница к голландскому математику Гюйгенсу в 1694 году. В обычное употребление термин введен в начале XVIII в. Иоганном Бернулли. Одно из первых определений понятия функции принадлежит также Леонарду Эйлеру (1707- 1783);

Запишем определение, четко разграничивая признаки понятия и выделим союз, который их соединяет.

Возрастающая функция- это

Ø Функция;

Ø у которой для любых двух значений аргумента из некоторого промежутка;

Ø большему значению аргумента соответствует большее значение функции.

Признаки должны выполняться вместе и соединены союзом «и».

Примеры возрастающей функции:

Рис. 13 Рис. 14