
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
I. Кинетика химических реакций
|
|
1.1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Химическая кинетика – раздел физической химии, изучающий скорости протекания химических реакций, их механизм и факторы, влияющие на скорость реакций. Скорость химической реакции определяется изменением количества одного из реагентов или продуктов реакции в единицу времени в единице реакционного пространства. Отсюда скорость реакции
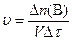 , (1)
, (1)
где 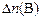 – изменение количества вещества
– изменение количества вещества 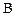 , моль, за промежуток времени реакции
, моль, за промежуток времени реакции 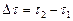 , с-1;
, с-1; 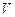 – объем системы, л.
– объем системы, л.
Учитывая, что молярная концентрация вещества 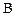
 моль/л, (2)
моль/л, (2)
то изменение молярной концентрации
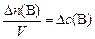 , моль/л;, (3)
, моль/л;, (3)
и, соответственно, получаем среднюю скорость реакции за промежуток времени 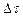 :
:
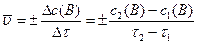 , (4)
, (4)
где знак (+) относится к изменению концентрации продуктов реакции, знак (-) – к изменению концентрации реагентов.
В уравнении химической реакции:
 (5)
(5)
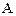 ,
, 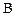 – реагенты – вещества, вступающие в реакцию;
– реагенты – вещества, вступающие в реакцию;
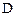 ,
, 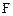 – продукты – вещества, образующиеся в результате реакции;
– продукты – вещества, образующиеся в результате реакции;
 ,
,  ,
, 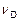 ,
, 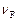 – стехиометрические коэффициенты, показывающие, какое количество соответствующего вещества участвует в реакции.
– стехиометрические коэффициенты, показывающие, какое количество соответствующего вещества участвует в реакции.
В ходе реакции концентрации веществ все время меняются, поэтому в химической кинетике рассматривают истинную, или мгновенную скорость реакции (в данный момент времени) и выражают ее первой производной концентрации вещества по времени:
 (6)
(6)
Скорость химической реакции зависит от многих факторов: от природы реагирующих веществ, концентрации, температуры, присутствия катализаторов, давления (в реакциях с участием газов).
Под природой реагирующих веществ понимают реакционную способность этих веществ, которая, так же как физические и химические свойства веществ, зависит от их состава, строения и внутримолекулярных связей.
1.2 ЗАКОН ДЕЙСТВУЮЩИХ МАСС
Влияние концентрации веществ на скорость реакции определяется законом действующих масс: при постоянной температуре скорость гомогенной химической реакции пропорциональна произведению концентраций реагирующих веществ, возведенных в степени, равные стехиометрическим коэффициентам в уравнении реакции.
Закон действующих масс для прямой гомогенной реакции,
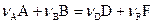 (7)
(7)
протекающей слева направо в однородной среде (смесь газов, раствор) (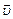 ), имеет вид:
), имеет вид:
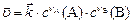 (8)
(8)
Для гетерогенной реакции, протекающей на границе раздела фаз (твердой и жидкой, твердой и газообразной) концентрации веществ, находящихся в конденсированном состоянии, постоянны и включаются в константу скорости реакции. Тогда для прямой реакции
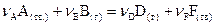 , (9)
, (9)
если вещество 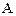 твердое, закон действующих масс запишется:
твердое, закон действующих масс запишется:
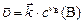 (10)
(10)
Для обратимых химических реакций, которые могут протекать как в прямом, так и в обратном направлениях, скорости реакции (5) запишутся:
Таблица 1
| Вид реакции | скорость реакции | |
прямой (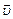 ) )
| обратной ( ) )
| |
| Гомогенная | 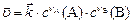
| 
|
Гетерогенная: вещества 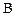 и и 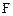 твердые или
жидкие твердые или
жидкие
| 
| 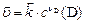
|
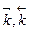 – константы скоростей прямой и обратной реакций, соответственно. Физический смысл константы скорости: при концентрации всех реагирующих веществ, равных 1 моль/л, константа скорости равна скорости реакции.
– константы скоростей прямой и обратной реакций, соответственно. Физический смысл константы скорости: при концентрации всех реагирующих веществ, равных 1 моль/л, константа скорости равна скорости реакции.
Константа скорости реакции зависит от природы реагирующих веществ, температуры и присутствия катализатора. Для каждой реакции при постоянной температуре константа скорости величина постоянная.
Используя закон действующих масс, можно определить, как будет изменяться скорость реакции при изменении параметров системы: 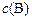 ,
, 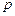 ,
, 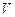 .
.
Пример 1. Для гомогенной газофазной реакции

определить: а) во сколько раз изменится скорость прямой реакции, если концентрацию азота уменьшить в 2 раза, а концентрацию водорода увеличить в 2 раза; б) давление в системе увеличить в 3 раза.
Решение. а) Согласно закону действующих масс, скорость прямой химической реакции описывается уравнением
 .
.
После изменения концентрации реагентов будут равны
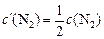 ;
; 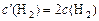 , тогда
, тогда
 , или
, или
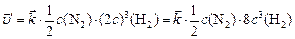 .
.
Изменение скорости прямой реакции по отношению к первоначальной:
 ,
,
т. е. скорость прямой реакции увеличится в 4 раза.
б) Из уравнения состояния газов (уравнение Менделеева-Клапейрона)
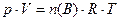 (11)
(11)
следует с учетом (2):
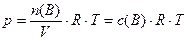 , (12)
, (12)
что 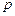 (при
(при 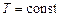 ) прямо пропорционально молярной концентрации газообразных веществ.
) прямо пропорционально молярной концентрации газообразных веществ.
Следовательно, увеличение (или уменьшение) давления в системе в 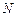 раз приводит соответственно к увеличению (или уменьшению) концентрации всех газов-участников реакции также в
раз приводит соответственно к увеличению (или уменьшению) концентрации всех газов-участников реакции также в 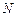 раз.
раз.
Тогда по условию задачи при увеличении давления в 3 раза новые концентрации веществ (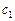 ):
):
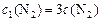 ;
; 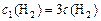 ,
,
тогда 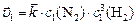 или
или
 ,
,
откуда:  ,
,
т. е. скорость прямой реакции увеличится в 81 раз.
Пример 2. Для реакции 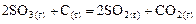 определите: а) как был изменен объем системы, если скорость прямой реакции уменьшилась в 4 раза? б) во сколько раз при этом изменилась скорость обратной реакции?
определите: а) как был изменен объем системы, если скорость прямой реакции уменьшилась в 4 раза? б) во сколько раз при этом изменилась скорость обратной реакции?
Решение. а) Прямая реакция гетерогенная, концентрация твердого углерода не входит в выражение скорости реакции, поэтому:
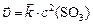 ,
,
или, учитывая:
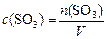 ,
,
получаем:
 .
.
Обозначим новый объем  ; так как количество
; так как количество  в системе не меняется, то
в системе не меняется, то
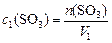 ,
,
и 
По условию задачи 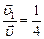 , откуда
, откуда
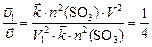 ;
;
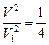 или
или  , т. е.
, т. е. 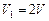 .
.
Следовательно, объем системы увеличился в 2 раза ( ).
).
б) Поскольку молярная концентрация вещества обратно пропорциональна объему системы (уравнение 2), то при увеличении объема в 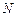 раз концентрации газообразных и растворенных веществ уменьшаются в
раз концентрации газообразных и растворенных веществ уменьшаются в 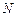 раз, а при уменьшении объема системы в
раз, а при уменьшении объема системы в 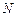 раз концентрации этих веществ увеличиваются в
раз концентрации этих веществ увеличиваются в 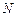 раз.
раз.
Если объем системы увеличился в 2 раза, то для обратной гомогенной реакции закон действующих масс запишется:
до изменения объема:
 ;
;
после увеличения объема в 2 раза:
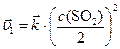
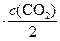 .
.
И тогда отношение скоростей будет равно:

Таким образом, скорость обратной реакции уменьшилась в 8 раз.
1.3 ИЗМЕНЕНИЕ КОНЦЕНТРАЦИЙ ВЕЩЕСТВ И СКОРОСТЕЙ В ХОДЕ РЕАКЦИИ
В ходе гомогенной реакции
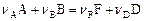
концентрации реагентов  и
и  уменьшаются, а концентрации продуктов
уменьшаются, а концентрации продуктов 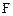 и
и 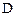 увеличиваются по сравнению с первоначальными значениями
увеличиваются по сравнению с первоначальными значениями  и в некоторый момент времени
и в некоторый момент времени 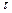 равны:
равны:
| для реагентов | для продуктов | ||
 
| (13) | 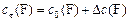
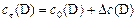
| (14) |
Как правило, в начальный момент времени концентрации продуктов реакции  равны нулю (
равны нулю ( ).
).
Изменения концентраций  для каждого вещества-участника реакции связаны со стехиометрическими коэффициентами в уравнении реакции:
для каждого вещества-участника реакции связаны со стехиометрическими коэффициентами в уравнении реакции:
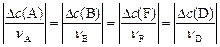 (15)
(15)
В соответствии с вышеизложенным различают скорости реакции:  – начальную и
– начальную и 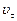 – в любой момент времени.
– в любой момент времени.
Таблица 2
| Скорость | Реакции | |
| прямая | обратная | |
начальная, 
| 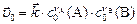
| 
|
в момент 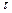 , , 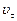
| 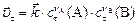
| 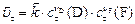
|
Используя уравнения (13 – 15) и таблицу 2, можно рассчитать концентрации и скорости реакций в любой момент времени.
Пример 3. Начальные концентрации реагентов газофазной реакции

равны (моль/л):  ;
; 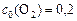 . Рассчитать: а) во сколько раз по сравнению с первоначальной изменится скорость прямой реакции в тот момент, когда прореагирует 20% сероуглерода. б) скорость обратной реакции в этот момент времени, если
. Рассчитать: а) во сколько раз по сравнению с первоначальной изменится скорость прямой реакции в тот момент, когда прореагирует 20% сероуглерода. б) скорость обратной реакции в этот момент времени, если 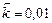 моль-2·л2·с-1.
моль-2·л2·с-1.
Решение. Для ответа на поставленные в задаче вопросы необходимо рассчитать:


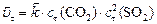
с0, сτ иΔ с связаны между собой соотношениями:

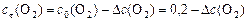
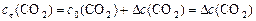 ,
,
а т.к 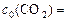
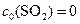 ,
,
то  .
.
Задача сводится в основном к определению изменения концентраций веществ, участвующих в реакции.
Для наглядности внесем исходные данные в таблицу.
Таблица 3
  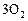  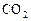  
| ||||
 , моль , моль
| ||||
 , моль/л , моль/л
| 0, 2 | 0, 2 | ||
 , моль/л , моль/л
| ||||
 , моль/л , моль/л
| ||||
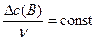
|
По мере определения указанных в таблице величин будем вносить их значения в таблицу. Значения обозначаем *.
или:
По условию задачи прореагировало 20%  . Чтобы определить
. Чтобы определить  , составляем пропорцию:
, составляем пропорцию:
с 0(CS2) = 0, 2 моль/л – 100%
Δ с (CS2) – 20%,
откуда
 моль/л.
моль/л.
Находим  - изменение концентрации реагентов и продуктов в ходе реакции, используя соотношение (15), записываем.
- изменение концентрации реагентов и продуктов в ходе реакции, используя соотношение (15), записываем.
 ,
,
откуда:
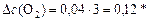 моль/л;
моль/л;
 моль/л;
моль/л;
 моль/л.
моль/л.
Вычисляем концентрации реагентов и продуктов в момент времени 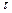 :
:
Реагенты:
 моль/л.
моль/л.
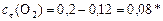 моль/л.
моль/л.
Продукты:
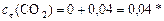 моль/л.
моль/л.
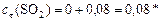 моль/л.
моль/л.
Ниже представлен окончательный вариант таблицы 3 с результатами расчетов.
Таблица 4
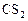  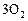  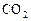  
| ||||

| ||||
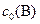 , моль/л , моль/л
| 0, 2 | 0, 2 | ||
 , моль/л , моль/л
| 0, 04 | 0, 12 | 0, 04 | 0, 08 |
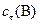 , моль/л , моль/л
| 0, 16 | 0, 08 | 0, 04 | 0, 08 |
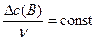
| 0, 04 | 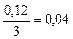
| 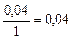
| 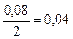
|
а) Вычисляем, во сколько раз изменится скорость прямой реакции в момент времени 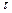 по сравнению с первоначальной.
по сравнению с первоначальной.
 .
.
Итак, скорость прямой реакции уменьшится в 19, 53 раза.
б) Рассчитаем скорость обратной реакции
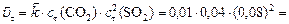

 .
.
Пример 4. Начальная концентрация оксида азота (I) в реакции

составляет 0, 7 моль/л, константа скорости прямой реакции  . Определить скорость прямой реакции в тот момент времени, когда образовалось 0, 3 моль/л диоксида углерода; массовую долю прореагировавшего оксида азота (I), а также концентрацию образовавшегося азота в этот момент.
. Определить скорость прямой реакции в тот момент времени, когда образовалось 0, 3 моль/л диоксида углерода; массовую долю прореагировавшего оксида азота (I), а также концентрацию образовавшегося азота в этот момент.
Решение. Для решения задачи необходимо: а) рассчитать скорость прямой гетерогенной реакции в момент 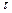 :
: 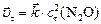 ; б) концентрацию продукта реакции (
; б) концентрацию продукта реакции (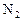 ) в момент
) в момент 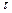 :
:  ; в) массовую долю прореагировавшего диоксида углерода (
; в) массовую долю прореагировавшего диоксида углерода (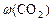 ).
).
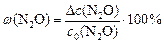
По условию задачи
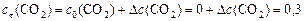 моль/л;
моль/л;
 моль/л.
моль/л.
Тогда, пользуясь соотношением (15), запишем:
 ,
,
определяем:
а) 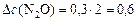 моль/л;
моль/л;
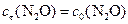
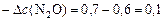 моль/л;
моль/л; 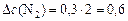 моль/л;
моль/л;  моль/л.
моль/л.
Результаты расчетов представим в виде таблицы 5.
Таблица 5
| С(ТВ.) + 2N2O(Г) = СО2 (Г) + 2N2 (Г) | ||||

| ||||
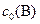 , моль/л , моль/л
| – | 0, 7 | ||
 , моль/л , моль/л
| – | 0, 6 | 0, 3 | 0, 6 |
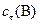 , моль/л , моль/л
| – | 0, 1 | 0, 3 | 0, 6 |
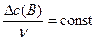
| – | 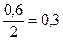
| 
| 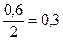
|
б) скорость прямой реакции в момент времени τ:

 .
.
в) массовая доля прореагировавшего N2O:
 .
.
Пример 5. Константа скорости гомогенной реакции
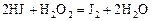
равна  . Через некоторое время от начала реакции в реакционной смеси обнаружено 20 % от первоначального количества HJ, 0, 2 моль/л
. Через некоторое время от начала реакции в реакционной смеси обнаружено 20 % от первоначального количества HJ, 0, 2 моль/л 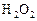 и 0, 4 моль/л
и 0, 4 моль/л 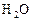 . Рассчитать концентрацию
. Рассчитать концентрацию 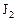 в этот момент и начальную скорость прямой реакции.
в этот момент и начальную скорость прямой реакции.
Решение. Известна концентрация одного из продуктов реакции – 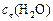 , что позволяет вычислить изменение концентрации
, что позволяет вычислить изменение концентрации  к моменту времени
к моменту времени 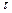 :
:
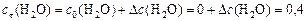 моль/л;
моль/л;
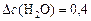 моль/л.
моль/л.
Тогда, пользуясь соотношением (15)
 ,
,
определяем:
 (моль/л);
(моль/л);
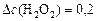 (моль/л);
(моль/л);
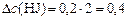 (моль/л).
(моль/л).
Искомая концентрация 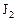 в момент времени
в момент времени 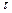 :
:
 моль/л;
моль/л;
Находим начальные концентрации реагентов.
Поскольку  , то
, то
 моль/л.
моль/л.
О втором реагенте (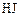 ) известно, что в реакционной смеси обнаружено (
) известно, что в реакционной смеси обнаружено (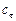 ) 20 % от первоначального количества; значит, прореагировало (
) 20 % от первоначального количества; значит, прореагировало ( ) 80 %. Составляем пропорцию:
) 80 %. Составляем пропорцию:
С0(HI) – 100%
Δ c(HI) = 0, 4 моль/л – 80%
откуда
 (моль/л).
(моль/л).
Начальную скорость прямой реакции рассчитываем по закону действующих масс:
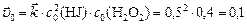
 .
.
Результаты расчетов представим в виде таблицы 6.
Таблица 6
    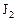  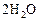
| ||||

| ||||
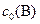 , моль/л , моль/л
| 0, 5 | 0, 4 | ||
 , моль/л , моль/л
| 0, 4 | 0, 2 | 0, 2 | 0, 4 |
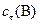 , моль/л , моль/л
| 0, 1 | 0, 2 | 0, 2 | 0, 4 |
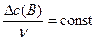
| 
| 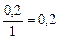
| 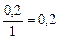
| 0, 2 |
Пример 6. В результате протекания реакции
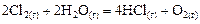
в реакционном сосуде объемом 5 л к некоторому моменту времени образовалось 71 г 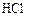 , осталось 0, 4 моль
, осталось 0, 4 моль 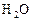 , а хлора прореагировало в 2 раза больше, чем осталось. Рассчитать концентрацию образовавшегося кислорода и скорость прямой реакции, если
, а хлора прореагировало в 2 раза больше, чем осталось. Рассчитать концентрацию образовавшегося кислорода и скорость прямой реакции, если  .
.
Решение. Вычислим концентрацию продуктов реакции:
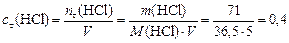 моль/л.
моль/л.
Поскольку  моль/л,
моль/л,
 моль/л.
моль/л.
Тогда, пользуясь соотношением (15) записываем:
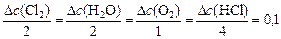 ,
,
определяем:
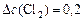 моль/л;
моль/л;
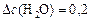 моль/л;
моль/л;
 моль/л.
моль/л.
Искомая концентрация кислорода в момент времени  :
:
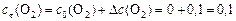 моль/л.
моль/л.
Находим начальные концентрации реагентов. Для этого сначала определяем концентрацию воды в момент времени 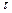 :
:
 моль/л,
моль/л,
Поскольку 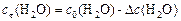 , то начальная концентрация воды
, то начальная концентрация воды
 моль/л.
моль/л.
По условию задачи, хлора прореагировало в 2 раза больше, чем осталось:
 ,
,
откуда концентрация хлора в момент времени 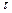 :
:
 моль/л.
моль/л.
Учитывая, что  , определяем начальную концентрацию хлора:
, определяем начальную концентрацию хлора:
 моль/л. Рассчитываем скорость прямой реакции в начальный момент времени:
моль/л. Рассчитываем скорость прямой реакции в начальный момент времени:

 ;
;
скорость прямой реакции в момент времени 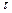 :
:
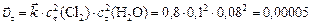
 .
.
Результаты расчетов представим в виде таблицы 7.
Таблица 7
| ||||

| ||||
 , моль/л , моль/л
| 0, 3 | 0, 28 | ||
 , моль/л , моль/л
| 0, 2 | 0, 2 | 0, 4 | 0, 1 |
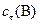 , моль/л , моль/л
| 0, 1 | 0, 08 | 0, 4 | 0, 1 |
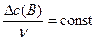
| 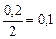
| 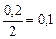
| 0, 1 | 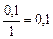
|
1.4 ЗАВИСИМОСТЬ СКОРОСТИ РЕАКЦИИ ОТ ТЕМПЕРАТУРЫ
1.4.1 Правило Вант-Гоффа
С повышением температуры скорость реакции увеличивается. Зависимость скорости реакции от температуры приближенно описывается эмпирическим правилом Вант-Гоффа: при повышении температуры на каждые 10° скорость реакции увеличивается в 2-4 раза.
Математическое выражение правила Вант-Гоффа:
 (16),
(16),
а при условии, что концентрации всех реагирующих веществ равны 1 моль/л:
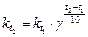 (17),
(17),
где  ,
,  и
и  ,
, 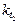 - соответственно скорости и константы скоростей реакции при температурах
- соответственно скорости и константы скоростей реакции при температурах 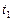 и
и 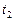 .
.
Температура может быть выражена как в °С, так и в К, так как изменение температуры не зависит от единиц измерения ( ).
).
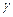 - температурный коэффициент скорости реакции, который показывает, во сколько раз возрастает скорость реакции при повышении температуры на 10 градусов:
- температурный коэффициент скорости реакции, который показывает, во сколько раз возрастает скорость реакции при повышении температуры на 10 градусов:
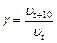 (18)
(18)
Поскольку при концентрациях реагирующих веществ 1 моль/л скорость химической реакции численно равна константе скорости 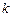 , то
, то
 (19)
(19)
Учитывая тот факт, что скорость реакции обратно пропорциональна времени ее протекания из уравнения (18), при  получаем
получаем
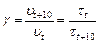 (20)
(20)
Используя уравнения (16 – 20), можно рассчитать:
- константу скорости (или скорость) реакции при заданной температуре, если известны значения этих величин при двух других температурах;
- на сколько градусов надо повысить (или понизить) температуру реакции, чтобы скорость ее увеличилась (или уменьшилась) в N раз;
- при какой температуре следует проводить реакцию, чтобы она закончилась за определенное время, если известны температурный коэффициент реакции и скорость ее при любой температуре;
- температурный коэффициент реакции и т. д.
Пример 7. Рассчитайте константу скорости химической реакции при 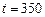 °С, если константа скорости этой реакции при температурах 400 °С и 500 °С равна соответственно 0, 03 и 50, 3.
°С, если константа скорости этой реакции при температурах 400 °С и 500 °С равна соответственно 0, 03 и 50, 3.
Решение
а). Для определения 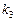 запишем уравнение Вант-Гоффа (17), используя
запишем уравнение Вант-Гоффа (17), используя 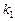 или
или 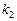 :
:
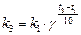 или
или 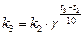
Учитывая:
 ,
, 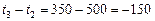 , получаем:
, получаем:
 или
или  (21)
(21)
б). Температурный коэффициент 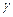 рассчитываем из отношения
рассчитываем из отношения 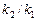 , полученного из уравнения (17):
, полученного из уравнения (17):
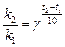


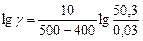
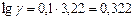
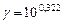
 .
.
в) 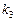 рассчитываем, подставляя полученное значение
рассчитываем, подставляя полученное значение 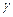 в уравнения (21):
в уравнения (21):
а) 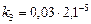

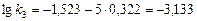
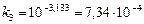
или
б) 
Ответ:  при
при 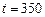 °С.
°С.
Пример 8. На сколько градусов надо повысить температуру реакции, чтобы скорость ее увеличилась в 15 раз, если  .
.
Решение. Из математического выражения правила Вант-Гоффа (16) и условия задачи получаем:
 , откуда
, откуда
 (22)
(22)
Логарифмируя уравнение (22), получаем формулу для определения  :
:
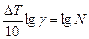
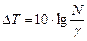 (23)
(23)
Подставляя в (23) условия задачи, получаем:
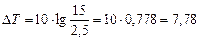 °
°
Ответ: Температуру реакции надо повысить на 7, 78 °.
Примечание: Если известна температура ( ), при которой проводилась реакция ранее, то используя полученные данные, можно рассчитать температуру (
), при которой проводилась реакция ранее, то используя полученные данные, можно рассчитать температуру (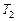 ), при которой следует проводить реакцию, чтобы скорость ее увеличилась в N раз:
), при которой следует проводить реакцию, чтобы скорость ее увеличилась в N раз:
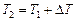 .
.
Пример 9. Сколько времени потребуется для проведения реакции при температуре 348 °К, если при температуре 298 °К она заканчивается за 30 минут;  .
.
Решение
1. Из правила Вант-Гоффа (16) следует:
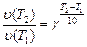 (24)
(24)
2. Поскольку скорость реакции обратно пропорциональна времени (1, 4), то
 (25)
(25)
3. Из (24), (25) получаем:
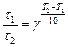 ,
, 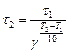

Таким образом, при  К реакция закончится за 0, 94мин.
К реакция закончится за 0, 94мин.
1.4.2. Уравнение Аррениуса
Более точно зависимость константы скорости реакции от температуры описывается уравнением Аррениуса:
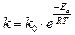 , (26)
, (26)
Если при изменении температуры концентрация реагентов остается постоянной, то зависимость скорости реакции от температуры описывается уравнением:
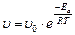 , где (27)
, где (27)
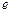 - основание натурального логарифма;
- основание натурального логарифма;
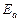 - энергия активации реакции, Дж/моль;
- энергия активации реакции, Дж/моль;
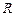 - универсальная газовая постоянная,
- универсальная газовая постоянная,  Дж/моль·К;
Дж/моль·К;
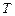 - температура, К;
- температура, К;
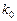 - предэкспоненциальный множитель;
- предэкспоненциальный множитель;
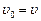 при
при  .
.
Энергия активации – это минимальная дополнительная или избыточная энергия по сравнению со средней энергией реагирующих частиц, которой должны обладать соударяющиеся частицы, чтобы вступить в реакцию. Частицы, обладающие такой энергией, называются активными. Энергия активации процесса зависит от природы реагирующих веществ. Значения энергии активации для химических реакций могут составлять от 40 до 200 кДж/моль. По гипотезе Аррениуса химическое взаимодействие осуществляется только при соударении активных частиц, доля которых в системе пропорциональна величине  . С увеличением температуры доля этих частиц в системе растет и соответственно растет скорость реакции.
. С увеличением температуры доля этих частиц в системе растет и соответственно растет скорость реакции.
Используя уравнение Аррениуса можно рассчитать:
- 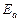 и
и 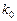 реакции, если известны константы скорости реакции при двух температурах;
реакции, если известны константы скорости реакции при двух температурах;
- константу скорости реакции при заданной температуре, если известны энергия активации реакции и константа скорости при какой-либо температуре.
Скорости при нескольких температурах можно рассчитать двумя способами.
Пример 10. Рассчитайте энергию активации процесса, если известно:
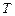 , К , К
| |||
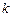 , с-1 , с-1
| 0, 0103 | 0, 02447 | 0, 05803 |
Решение. 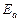 рассчитываем, используя уравнение Аррениуса (26) для двух температур:
рассчитываем, используя уравнение Аррениуса (26) для двух температур:
 и
и 
Откуда:
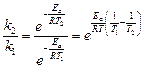
Прологарифмировав последнее уравнение, с учетом того, что 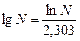 получаем:
получаем:
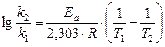
и, соответственно:

Для 726 К и 746 К:
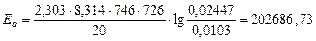 Дж/моль.
Дж/моль.
Для 726 К и 766 К:
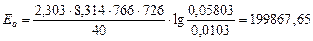 Дж/моль.
Дж/моль.
Для 746 К и 766 К:
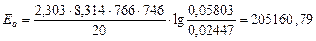 Дж/моль.
Дж/моль. 
Средняя энергия активации равна 
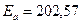 кДж/моль.
кДж/моль.
Пример 11. Рассчитайте 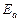 и
и 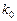 процесса, если известны константы скоростей реакции при различных температурах.
процесса, если известны константы скоростей реакции при различных температурах.
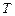 , К , К
| |||
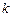 , л·моль-1·мин-1 , л·моль-1·мин-1
| 2, 43 | 10, 53 | 21, 9 |
Решение. 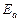 ,
, 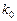 определяем графическим методом, используя логарифмическую форму уравнения Аррениуса (26):
определяем графическим методом, используя логарифмическую форму уравнения Аррениуса (26):
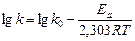 (28)
(28)
Для этого представим экспериментальные данные в следующем виде:
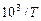
| 3, 53 | 3, 30 | 3, 19 |
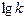
| 0, 38 | 1, 02 | 1, 34 |
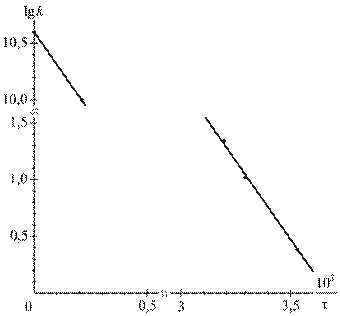
На их основе строим график зависимости 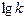 от
от 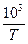 (см. рис. 1).
(см. рис. 1).
Из рис.1, согласно уравнению (26)

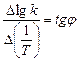 находим из графика:
находим из графика:
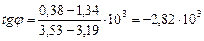
 Дж/моль.
Дж/моль.
Из уравнения (24) следует:
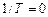 .
.  .
.
Продлив график до пересечения с осью 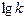 , получаем
, получаем

 .
.
Таким образом: 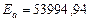 Дж/моль,
Дж/моль,  .
.
Приложение 1
| Федеральное агентство по образованию Новосибирский государственный архитектурно-строительный университет Кафедра химии Индивидуальное задание по химии Работу выполнил студент: ______________________ группа_____ «___»____________2009 г. Работу проверил преподаватель: ________________________ «___»____________2009 г. Новосибирск 2009 |
|