
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Движение заряженной частицы в магнитном поле
|
|
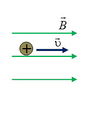
- Если скорость υ заряженной частицы массой m направлена вдоль вектора магнитной индукции поля, то частица будет двигаться по прямой с постоянной скоростью (сила Лоренца F L = 0, т.к. α = 0°) (рис. 9 а).
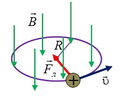
- Если скорость υ заряженной частицы массой m перпендикулярна вектору магнитной индукции поля, то частица будет двигаться по окружности радиуса R, плоскость которой перпендикулярна линиям магнитной индукции (рис. 9 б). Тогда 2-ой закон Ньютона можно записать в следующем виде:
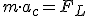 ,
,
где 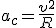 ,
, 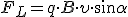 , α = 90°, т.к. скорость частицы перпендикулярна вектору магнитной индукции.
, α = 90°, т.к. скорость частицы перпендикулярна вектору магнитной индукции.
Тогда 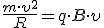 .
.
 а
а
|  б
б
|
Рис. 9
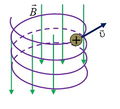
3. Если скорость υ заряженной частицы массой m направлена под углом α (0 < α < 90°) к вектору магнитной индукции поля, то частица будет двигаться по спирали радиуса R и шагом h (рис. 10 а, в).
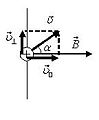
Для описания движения частицы можно использовать следующий способ: разложить скорость υ заряженной частицы на две составляющие υ ⊥ = υ ·sin α – перпендикулярную (к линии индукции) и υ || = υ ·cos α – параллельную (к линии индукции) (рис. 10 б). Перпендикулярная составляющая скорости υ ⊥ вызывает движение частицы по окружности радиуса R, плоскость которой перпендикулярна линиям магнитной индукции, а параллельная υ || – равномерное движение вдоль линии индукции (рис. 10 в).
 а
а
|  б
б
|  в
в
|
Рис. 10
Для описания движения по окружности, перпендикулярно линиям магнитной индукции, используем уравнение 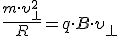 или
или 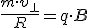 , т.к.
, т.к. 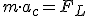 , где
, где 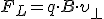 ,
, 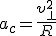 .
.
Для описания движения вдоль линий магнитной индукции, используем уравнение h = υ ||· T, где h – это шаг винтовой линии (спирали), Т – время, за которое частица совершит полный оборот (период).