
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Знакоопределенные квадратичные формы
|
|
В этом параграфе и до конца главы мы будем рассматривать квадратичные формы только на действительных линейных пространствах.
Определения. Квадратичная форма называется положительно определенной, если она принимает положительные значения для любого нетривиального набора переменных.
Квадратичная форма называется отрицательно определенной, если она принимает отрицательные значения для любого нетривиального набора переменных.
Квадратичная форма называется положительно (отрицательно) полуопределенной, если для любого нетривиального набора переменных она принимает либо положительное (отрицательное) значение, либо 0.
Квадратичная форма знаконеопределена, если существует нетривиальный набор переменных, при которых она принимает положительное значение, и существует нетривиальный набор переменных, при которых она принимает отрицательное значение.
Лемма 5.3. Эквивалентные квадратичные формы принимают одинаковые значения при соответствующих наборах переменных.
► Пусть квадратичные формы 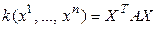 и
и 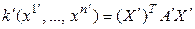 эквивалентны. Это значит, что существует линейное невырожденное преобразование переменных
эквивалентны. Это значит, что существует линейное невырожденное преобразование переменных 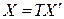 , переводящее квадратичную форму
, переводящее квадратичную форму 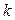 в квадратичную форму
в квадратичную форму 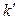 . Тогда по теореме 5.5
. Тогда по теореме 5.5 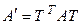 , значит,
, значит,
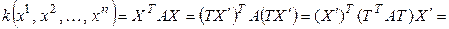
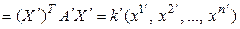 .◄
.◄
Следствие. Если квадратичная форма положительно определена, то все эквивалентные ей квадратичные формы также положительно определены.
Лемма 5.4 (необходимое условие знакоопределенност и). Если квадратичная форма положительно (отрицательно) определена, то все ее коэффициенты при квадратах положительны (отрицательны).
► Пусть квадратичная форма
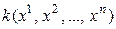 =
= 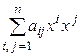
положительно определена. Тогда 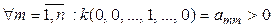 (единица на m -м месте), следовательно, все коэффициенты при квадратах положительны.◄
(единица на m -м месте), следовательно, все коэффициенты при квадратах положительны.◄
Теорема 5.8 (первый критерий знакоопределенности). Для того чтобы квадратичная форма была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все коэффициенты какого-либо ее канонического вида были положительными (отрицательными).
► Пусть задана квадратичная форма и пусть
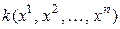 =
= 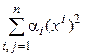 – (5.23)
– (5.23)
какой-либо ее канонический вид.
Необходимость. Дано: исходная квадратичная форма положительно определена. Тогда по следствию к лемме 5.3 форма (5.23) тоже положительно определена, а значит, по лемме 5.4 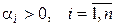 .
.
Достаточность. Дано: 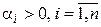 . Тогда, очевидно, для любого нетривиального набора переменных форма (5.23) принимает только положительные значения, следовательно, она положительно определена, и поэтому положительно определена и исходная квадратичная форма. ◄
. Тогда, очевидно, для любого нетривиального набора переменных форма (5.23) принимает только положительные значения, следовательно, она положительно определена, и поэтому положительно определена и исходная квадратичная форма. ◄
Следствие. Матрица положительно определенной квадратичной формы имеет положительный определитель.
► Пусть А – матрица положительно определенной квадратичной формы, А' – матрица ее канонического вида (5.23). При линейном невырожденном преобразовании переменных определитель матрицы квадратичной формы не меняет знака. Так как 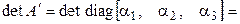
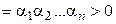 , то и
, то и 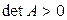 .◄
.◄