
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача №4
|
|
Даны коэффициенты прямых затрат 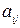 , конечный продукт Yi, для трехотраслевой экономической системы.
, конечный продукт Yi, для трехотраслевой экономической системы.
| Производящие отрасли | Коэффициент прямых затрат aij | Конечный продукт, Y | ||
| 0, 4 | 0, 3 | 0, 1 | ||
| 0, 1 | 0, 2 | 0, 4 | ||
| 0, 3 | 0, 4 | 0, 1 |
Требуется определить:
А) коэффициенты полных затрат;
Б) вектор валового выпуска;
В) межотраслевые поставки продукции;
Г) проверить продуктивность матрицы А;
Д) заполнить схему межотраслевого баланса;
Е) проверить, является ли экономика высокоэффективной.
Решение:
МЕЖОТРАСЛЕВОЙ БАЛАНС (МОБ) — каркасная модель экономики: таблица, в которой показываются многообразные натуральные и стоимостные связи в народном хозяйстве. Анализ МОБ дает комплексную характеристику процесса формирования и использования совокупного общественного продукта в отраслевом разрезе.
| Производящие отрасли | Потребляющие отрасли | Конечный продукт | Валовой продукт |
| 1 2 … n | |||
| … n | х11 х12 … х1n х21 х22 … х2n ……………………… хn1 хn2 … хnn | y1 y2 … yn | X1 X2 … Xn |
| Условно чистая прибыль | z1 z2 … zn |  yi= yi=  zj zj
| |
| Валовой продукт | X1 X2 … Xn |  xi= xi=  xj xj
|


Потребление вне производственной сферы задано вектором Y=Х-АХ, где
Х-АХ – это количество продукции, которое потребляется в непроизводственной сфере.
Следует ответить на вопрос: существует ли вектор Х, который это потребление обеспечивает, иначе существует ли решение уравнения Y=Х-АХ.
Модель Леонтьева продуктивна тогда и только тогда, если существует неотрицательная матрица, обратная к матрице (Е-А)-1 (по теореме).
Условие продуктивности для неразложимых матриц:
модель Леонтьева, с данной матрицей, продуктивна тогда, когда сумма элементов каждой строки не больше единицы и хотя бы для одной строки строго меньше единицы.
Сумма элементов в данной матрице А меньше единицы, значит матрица продуктивна, а это значит что существует обратная к ней матрица А-1.
Найдем коэффициенты полных затрат.
КОЭФФИЦИЕНТЫ ПОЛНЫХ ЗАТРАТ в межотраслевом балансе — суммарные затраты i-го продукта на производство единицы конечного продукта отрасли j по всей цепи сопряженных производств. Они складываются из прямых затрат каждой отрасли на данный продукт и косвенных затрат. Где прямые затраты - затраты, которые можно напрямую отнести на себестоимость определенного вида продукции. Косвенные затраты - затраты, которые нельзя напрямую отнести на себестоимость каждого конкретного продукта, выпускаемого предприятием: накладные расходы на материал, производственные накладные расходы, административные и торговые накладные расходы.
Иначе говоря, коэффициент полных затрат bij показывает потребность в валовом выпуске продукции отрасли i для производства единицы конечной продукции j-го вида. Каждой клеточке таблицы МОБ соответствует свой коэффициент полных затрат bij. Выписав их столбцами и строками в соответствии с этой таблицей, получим матрицу (таблицу) коэффициентов [bij]. В матричной записи ее принято обозначать буквой B.
Расчет полных затрат весьма сложен, требует значительной вычислительной работы. Есть два основных способа решения этой задачи: первый — подсчет косвенных затрат и их суммирование с прямыми, второй — непосредственное получение коэффициент полных затрат из матрицы коэффициентов прямых затрат с помощью операции, называемой обращением матрицы. В последнем случае решение системы уравнений МОБ приводит к матрице (таблице) коэффициентов полных затрат:
B = (E – A)–1.
Во многих случаях полные затраты существенно превышают прямые затраты: степень превышения связана с характером производства того или иного продукта.
Кроме того, в коэффициент полных затрат нередко отражена более широкая по сравнению с коэффициентами прямых затрат номенклатура учитываемых ресурсов: например, сырая нефть не употребляется непосредственно при производстве чугуна (коэффициент прямых затрат равен нулю), но в числе полных затрат она отражена (через использование энергии в транспорте).
В планировании рассчитываются также коэффициенты (нормативы) полных затрат труда и капитальных вложений, полная фондоемкость производства единицы продукции.
Использование системы коэффициент полных затрат позволяет быстро оценить, какие поправки необходимо внести в материальные ресурсы для обеспечения сбалансированности экономики. Они применяются также при оценке влияния изменений межотраслевых пропорций на эффективность производства.

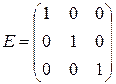
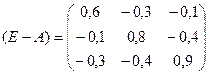
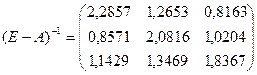

- коэффициенты полных затрат.
Найдем вектор валового выпуска.
Валовой выпуск продукции – объем производства отрасли i за данный промежуток времени. Вычислим вектор валового выпуска по формуле X=B*Y.

Найдем матрицу потребляющих отраслей
xij =aij*Xj:

Найдем условно чистую прибыль
Z= Xj- 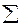 xij
xij
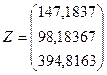
| Производящие отрасли | Потребляющие отрасли | Конечный продукт | Валовой продукт | ||
| 110, 2041 | 82, 65306 | 27, 55102 | 864, 0816 | ||
| 49, 59184 | 99, 18367 | 198, 3673 | 915, 102 | ||
| 121, 2245 | 161, 6327 | 40, 40816 | 939, 1837 | ||
| Условная чистая прибыль | 147, 1837 | 98, 18367 | 394, 8163 | 640=640 | |
| Валовой продукт | 864, 0816 | 915, 102 | 939, 1837 | 2718, 367 |
Проверим, является ли экономика высокоэффективной.
A- прямые затраты
X- валовой выпуск
C- конечное потребление
Экономика называется высокоэффективной, если увеличение выпуска X на 1% дает большую прибавку конечного потребления С, чем снижение прямых затрат аij на 1% и экономика называется низкоэффективной в противном случае.
С1=1, 01Х – А(1, 01Х) = 1, 01(Х-АХ)=1, 01С
∆ С1=0, 01С
С2=Х-0, 99АХ
∆ С2=1, 01АХ
∆ С2< ∆ С1 условие высокоэффективности экономики
0, 01АХ< 0, 01С



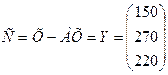
 Экономика является высокоэффективной.
Экономика является высокоэффективной.
|