Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Работа по перемещению проводника с током в магнитном поле. где - магнитный поток, пересеченный движущимся проводником.
|
|
,
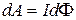где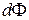 
- магнитный поток, пересеченный движущимся проводником.
25. Работа по перемещению замкнутого контура с током в магнитном поле
,
где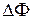 
- изменение магнитного потока, сцепленного с контуром.
26. Закон Фарадея: э.д.с. электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
.
Если контур состоит из N витков, то
,
где 
- потокосцепление, F - поток через один виток.
27. Индуктивность контура:
,
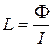где Ф - магнитный поток, сцепленный с контуром, I – ток в контуре.
28. Индуктивность соленоида:
,
где N - число витков в соленоиде, S - площадь, l –длина соленоида.
29. Э.д.с. самоиндукции при L = const:
.
30. Энергия магнитного поля, связанного с контуром:
.
31. Объемная плотность энергии:
.
3. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 1. Два заряда q 1= +4, 5 q и q 2= - 0, 5 q находятся на расстоянии l = 10 см. Третий заряд, модуль которого | q 3|= q, может перемещаться вдоль прямой, проходящей через заряды q 1 и q 2. Определите положение заряда q 3, при котором он будет находиться в равновесии.
Решение. Заряд q 3будет находиться в положении равновесия в точке пространства, где суммарная напряженность поля 
= 0. На отрезке, лежащем между зарядами q 1 и q 2 такой точки нет, т.к. векторы напряженности 
и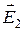 
электрический полей, создаваемых, соответственно, зарядами q 1 и q 2 направлены в одну сторону, и их сумма не может быть равной нулю.
В точках прямой, расположенных слева и справа от рассмотренного отрезка, векторы напряженности и 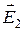направлены в противоположные стороны. Для того, чтобы их сумма равнялась нулю, необходимо, чтобы модули этих векторов были равны, т.е. Е 1 = Е 2. Учитывая, что 
, а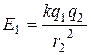 
, должно выполняться условие
.
Для любой точки, лежащей левее заряда q 1, расстояние r 1 меньше расстояния r 2. Поскольку по условию | q 1| > | q 2|, то Е 1 всегда больше, чем Е2. Точки с Е = 0 в этой части прямой нет.
Рассмотрим точки на прямой, расположенные правее заряда q 2. В этом случае r 1 = r 2 + l. В точке равновесия должно выполняться условие
,
приводящее к уравнению
.
Из этого уравнения находим, что точка равновесия находится на 5 см правее заряда q 2.
Равновесие заряда q 3будет устойчивым, если при смещении этого заряда вправо возникает сила, направленная влево, стремящаяся вернуть заряд в прежнее положение. При перемещении заряда влево, должна возникать сила, направленная вправо.
Предположим, что заряд q 3 положительный. Тогда в найденной нами точке равновесия сила F 1, действующая на заряд q 3со стороны положительного заряда q 1, направлена вправо, а сила F 2, действующая со стороны отрицательного заряда q 2 направлена влево.
При смещении заряда q 3 вправо увеличивается расстояние как r 2, так и r 1 = l+ r 2. В результате уменьшаются обе силы. Учитывая, что F 1 ~ 1/(l+ r 2 )2, а F 2 ~ 1/ r 2 2, можно сделать вывод, что с ростом r 2 сила F 1 убывает медленнее, чем сила F 2. В результате результирующая сила направлена вправо и стремиться удалить заряд q 3 еще дальше от точки равновесия. Равновесие неустойчивое.
Предположим теперь, что заряд q 3 - отрицательный. Теперь сила F1 будет направлена влево, а сила F2 - вправо.
 |
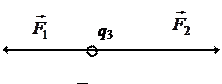В этом случае, при смещении заряда q 3 вправо, как и в предыдущем случае, F 1 убывает медленнее, чем F 2. Результирующая сила направлена влево и стремится вернуть заряд q 3 на прежнее место.
Рассмотрение смещения заряда q 3 влево приводит к тем же выводам. Таким образом, если заряд q 3отрицательный, то положение равновесия является устойчивым.
Пример 2. Внутри плоскопараллельной непроводящей пластины толщиной d равномерно распределен положительный заряд с объемной плотностью r. Пластина расположена перпендикулярно оси x. Плоскость симметрии пластины проходит через начало отсчета на оси х. Определить зависимость напряженности E от x как внутри, так и вне пластины. Построить графики зависимости Ex (проекции вектора на ось x) от x.
Решение. Для решения этой задачи воспользуемся теоремой Гаусса. Из соображений симметрии можно сделать следующий вывод:
а) 
,
б) напряженность поля Е одинакова во всех точках плоскости, перпендикулярной оси х,
в) силовые линии электрического поля параллельны оси х.
Полученные выводы позволяют выбрать форму замкнутой поверхности так, чтобы расчет потока вектора через нее осуществлялся наиболее просто. Такая поверхность может иметь, например, форму цилиндра. Основания цилиндра должны быть параллельны поверхности пластины. Образующие цилиндра должны быть параллельны оси х. Цилиндр должен быть расположен симметрично относительно пластины. В этом случае поток вектора через каждое из оснований цилиндра равен (E× s), где Е - напряженность поля в точках, лежащих на основании, s - площадь основания.
 |
Поток вектора через боковую поверхность цилиндра равен нулю, т.к. нормальная составляющая Еn к этой поверхности равна нулю. Таким образом, поток через всю замкнутую поверхность
ФЕ = ò Еn ds = 2 E× s