
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Повышенный уровень.
|
|
Экзаменационная программа по математическому анализу
в осеннем семестре 1-го курса. Поток Ковалева В.П.
Повышенный уровень.
1. Доказать: 
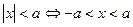 ;
; 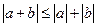 ;
; 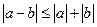 ;
; 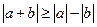 ;
; 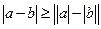 .
.
2. Определение точной верхней и точной нижней грани числового множества. Теорема о существовании точной верхней грани у непустого ограниченного сверху множества. Единственность точной верхней грани.
3. Счётные и несчетные множества. Счётность Q. Несчетность множества точек отрезка [0, 1].
4. Определение последовательности. Определение того, что число a является пределом последовательности. Построение отрицания. Теорема об ограниченности сходящейся последовательности. Единственность предела последовательности.
5. Свойства предела последовательности, связанные с неравенствами.
6. Теорема о существовании предела у монотонно возрастающей и ограниченной сверху последовательности. Число e.
7. Подпоследовательность последовательности. Верхний и нижний частичные пределы. Теорема о подпоследовательности сходящейся последовательности.
8. Теорема Больцано-Вейерштрасса.
9. Критерий Коши сходимости последовательности.
10. Бесконечно малые последовательности. Их свойства. Свойства последовательностей, связанные с арифметическими действиями.
11. Бесконечно большие последовательности и их свойства.
12. Два определения конечного предела функции при стремлении аргумента к числу и доказательство их эквивалентности.
13. Односторонние пределы. Обобщение понятия предела.
14. Свойства пределов функций, связанные с неравенствами и с арифметическими действиями.
15. Теорема о пределе сложной функции. Бесконечно малые и бесконечно большие функции.
16. Критерий Коши существования конечного предела функции в точке.
17. Теорема о существовании односторонних пределов у монотонной функции.
18. Непрерывность функции в точке. Односторонняя непрерывность. Точки разрыва 1-го и 2-го рода.
19. Непрерывность суммы, произведения, частного непрерывных в точке функций. Непрерывность сложной функции.
20. Теорема Вейерштрасса о непрерывной на отрезке функции.
21. Теорема Больцано-Коши о промежуточном значении для непрерывной на отрезке функции.
22. Теорема об обратной функции для строго монотонной и непрерывной на отрезке функции. Теорема об обратной функции в случае интервала и полуинтервала (формулировка).
23. Непрерывность многочленов, рациональных функций, корней, тригонометрических и обратных тригонометрических функций.
24. Показательная функция. Определение. Корректность определения. Свойства.
25. Определение и непрерывность логарифмической и степенной функций.
26. Непрерывность тригонометрических и обратных тригонометрических функций.
27. Доказать замечательные пределы: 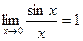 ,
, 
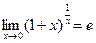 .
.
28. Доказать пределы: 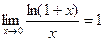 ,
, 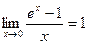 .
.
29. Определение символов: «о», «О», «~». Свойства функций, связанных этими символами.
30. Определение производной. Непрерывность в точке функции, имеющей в этой точке производную. Производная функций 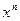 ,
, 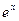 ,
, 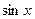 ,
, 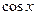 . Свойства производной, связанные с арифметическими действиями. Производные гиперболических функций. Односторонние производные. Бесконечные производные.
. Свойства производной, связанные с арифметическими действиями. Производные гиперболических функций. Односторонние производные. Бесконечные производные.
31. Производная обратной функции. Производные обратных тригонометрических функций, логарифмической функции.
32. Производная сложной функции. Производная параметрически заданной функции.
33. Определение дифференцируемости функции в точке. Теорема об эквивалентности дифференцируемости функции и существовании конечной производной. Дифференциал и его свойства. Инвариантность формы первого дифференциала.
34. Производные высших порядков. Формула Лейбница. Дифференциалы высших порядков.
35. Вторая производная функции, заданной параметрически.
36. Теоремы о среднем для дифференцируемых функций (теорема Ферма, теорема Ролля, теорема Лагранжа, теорема Коши).
37. Формулы Тейлора и Маклорена. Лемма о производной остаточного члена. Остаточный член формулы Тейлора в форме Пеано и Лагранжа. Единственность представления функции в виде суммы многочлена и остаточного члена в форме Пеано. Разложения по формуле Маклорена функций: 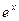 ,
, 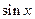 ,
, 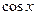 , sh x, ch x,
, sh x, ch x, 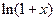 ,
, 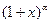 .
.
38. Правило Лопиталя для предела отношения двух бесконечно малых функций при стремлении аргумента к числу справа и к + 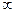 . Правило Лопиталя для предела отношения двух бесконечно больших функций при стремлении аргумента к числу справа.
. Правило Лопиталя для предела отношения двух бесконечно больших функций при стремлении аргумента к числу справа.
39. Достаточное условие строгой монотонности функции на интервале.
40. Необходимое условие экстремума. Достаточные условия строгого экстремума.
41. Достаточное условие строгой выпуклости функции на интервале.
42. Необходимое условие точки перегиба. Достаточное условие точки перегиба.
43. Вектор-функция, её предел, непрерывность, дифференцируемость, формула Тейлора, аналог теоремы Лагранжа.
44. Кривая в пространстве. Её носитель и представление. Касательная к кривой. Длина кривой. Спрямляемость непрерывно дифференцируемой кривой. Производная переменной длины дуги непрерывно дифференцируемой кривой.
45. Натуральное представление кривой. Кривизна кривой. Главный нормальный вектор. Бинормальный вектор. Центр кривизны кривой. Соприкасающаяся плоскость.
46. Формулы для кривизны кривой, для касательного, главного нормального и бинормального векторов дважды дифференцируемой кривой без особых точек при произвольном её представлении.
47. Неопределённый интеграл и его свойства. Интегрирование по частям и заменой переменной.
48. Комплексные числа. Алгебраическая и тригонометрическая формы. Определение экспоненты комплексного числа и её свойства.
49. Разложение многочлена на множители. Разложение правильной рациональной дроби на элементарные.
Кафедра высшей математики.