
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Достатність.
|
|
Нехай всі характеристичні корені матриці 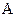 знаходяться в полі
знаходяться в полі 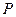 . Нехай нерівними
. Нехай нерівними 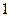 інваріантними множниками матриці
інваріантними множниками матриці 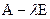 будуть
будуть
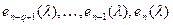 (9).
(9).
Тоді 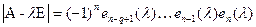 . Дійсно, визначники матриці
. Дійсно, визначники матриці 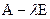 і її канонічної матриці можуть відрізнятися один від одного тільки сталим множником, який насправді дорівнює
і її канонічної матриці можуть відрізнятися один від одного тільки сталим множником, який насправді дорівнює 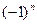 , оскільки саме такий старший коефіцієнт характеристичного многочлена
, оскільки саме такий старший коефіцієнт характеристичного многочлена 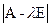 . Таким чином:
. Таким чином:
· серед многочленів (9) немає рівних 0;
· сума степенів цих многочленів рівна 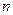 ;
;
· всі вони розкладаються над полем 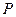 на лінійні множники (тому, що за умовою многочлен
на лінійні множники (тому, що за умовою многочлен 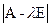 володіє таким розкладом).
володіє таким розкладом).
Нехай (8) будуть розклади многочленів (9) в добутки степенів лінійних множників. Назвемо елементарними дільниками многочлена 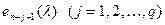 відмінні від
відмінні від 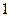 степені різних лінійних двочленів, які входять в його розклад (4), тобто
степені різних лінійних двочленів, які входять в його розклад (4), тобто 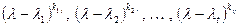 . Елементарні дільники всіх многочленів (9) називаються елементарними дільниками матриці
. Елементарні дільники всіх многочленів (9) називаються елементарними дільниками матриці 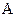 . Випишемо їх у вигляді таблиці (7).
. Випишемо їх у вигляді таблиці (7).
Утворимо тепер жорданову матрицю 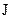 порядку
порядку 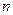 , складену із жорданових кліток, які визначаються так: кожному елементарному дільнику
, складену із жорданових кліток, які визначаються так: кожному елементарному дільнику 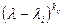 матриці
матриці 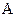 ставимо у відповідність жорданову клітку порядку
ставимо у відповідність жорданову клітку порядку 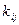 , яка відноситься до числа
, яка відноситься до числа 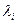 . Очевидно, що нерівними 1 інваріантними множниками матриці
. Очевидно, що нерівними 1 інваріантними множниками матриці 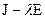 теж будуть многочлени (9) і тільки вони. Тому матриці
теж будуть многочлени (9) і тільки вони. Тому матриці 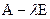 і
і 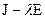 еквівалентні і, значить, матриця
еквівалентні і, значить, матриця 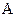 подібна жордановій матриці
подібна жордановій матриці 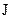 .▲
.▲
Наприклад: Нехай дана матриця 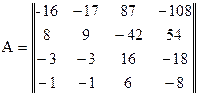 . Зводячи звичайним способом матрицю
. Зводячи звичайним способом матрицю 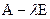 до канонічного вигляду, одержимо, що нерівними
до канонічного вигляду, одержимо, що нерівними 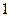 інваріантними множниками цієї матриці будуть многочлени
інваріантними множниками цієї матриці будуть многочлени 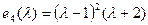 і
і 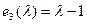 . Ми бачимо, що матриця
. Ми бачимо, що матриця 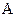 зводиться до жорданової нормальної форми навіть в полі раціональних чисел. Її елементарними дільниками є многочлени
зводиться до жорданової нормальної форми навіть в полі раціональних чисел. Її елементарними дільниками є многочлени 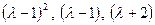 , а тому жордановою нормальною формою матриці
, а тому жордановою нормальною формою матриці 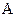 є матриця
є матриця 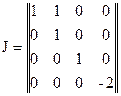 .
.
Необхідна і достатня умова зведення матриць до діагонального вигляду
На основі отриманих результатів може бути сформульована, нарешті, необхідна і достатня умова звідності матриць до діагонального вигляду.
Теорема 4. Матриця 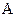 порядку
порядку 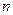 з елементами з поля
з елементами з поля 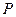 зводиться до діагональ-ного вигляду тоді і тільки тоді, якщо усі її характеристичні корені (або всі корені останнього інваріантного множника
зводиться до діагональ-ного вигляду тоді і тільки тоді, якщо усі її характеристичні корені (або всі корені останнього інваріантного множника 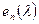 її характеристичної матриці) знаходяться в полі
її характеристичної матриці) знаходяться в полі 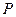 , причому серед цих коренів немає кратних.
, причому серед цих коренів немає кратних.
Доведення:
Дійсно, звідність матриці до діагонального вигляду рівносильна звідності до такого жорданового вигляду, всі жорданові клітки якого мають порядок 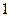 . Іншими словами, всі елементарні дільники матриці
. Іншими словами, всі елементарні дільники матриці 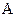 повинні бути многочленами 1-го степеня. Оскільки, однак, всі інваріантні множники матриці
повинні бути многочленами 1-го степеня. Оскільки, однак, всі інваріантні множники матриці 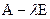 являються дільниками многочлена
являються дільниками многочлена 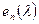 , то остання умова рівносильна тому, що всі елементарні дільники многочлена
, то остання умова рівносильна тому, що всі елементарні дільники многочлена 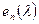 мають степінь
мають степінь 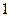 , що й треба довести.▲
, що й треба довести.▲