Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Справочная информация
|
|
| Уравнение | Кривая |
| x 2 + y 2 = R 2 | Окружность радиуса R с центром в начале координат |
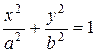
| Эллипс, оси которого лежат на осях координат. Горизонтальная ось эллипса равна 2 а, вертикальная ось равна 2 b |
| y 2 = 2 px | Парабола, ось которой совпадает с осью Х, фокус находится в точке (р /2, 0) |
| Y = ax 2 + c | Парабола, ось которой совпадает с осью Y, вершина (0, с) |
Отношения и логические операции, их старшинство
| Операция | Фортран-77 | Фортран-90 | Старшинство |
| Вычислить a, b | a и b –арифметические выражения либо a и b - строковые выражения | ||
| Больше чем | a.GT.b | a> b | |
| Больше или равно | а.GE.b | a> =b | |
| Меньше чем | а.LT.b | a< b | |
| Меньше или равно | а.LE.b | a< =b | |
| Тождество | а.EQ.b | a= =b | |
| Неравенство | а.NE.b | a/=b | |
| Инверсия | .NOT.n | .NOT.n | |
| Логическое И | k.AND.n | k.AND.n | |
| Логическое ИЛИ | k.OR.n | k.OR.n | |
| Эквивалентность | k.EQV.n | k.EQV.n | |
| Неэквивалентность | k.NEQV.n | k.NEQV.n |
Примечания: k, n –логические выражения
если a, b- строки, то они сравниваются как в словаре
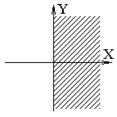
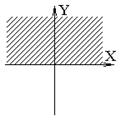
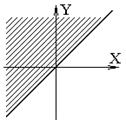
Пример Рассмотрим три неравенства: x ≥ 0, y ≥ 0, y ≥ x.
Графическая интерпретация неравенств и запись на Фортране соответствующих отношений показаны в таблице:
| x ≥ 0 | y ≥ 0 | y ≥ x |
| 
| 
|
| x> =0 | y> =0 | y> =x |
То, что границы для строгих неравенств не входят в область, следует обозначать пунктиром, вместо сплошных линий.
Соединив отношения логическими операциями .OR. и .AND., получим два логических выражения:
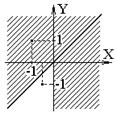
iLi = x .GT. 0.0 .OR. y .GT. 0.0 .OR. y .GT. x истинно для точек в I или II или IV квадрантах или выше прямой y=x
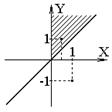
i = x .GT. 0.0 .AND. y .GT. 0.0 .AND. y .GT. x истинно для точек в I квадранте и выше прямой y = x
Графическая интерпретация условий, соответствующих этим выражениям, и координаты выбранных точек представлены в таблице:
| Логическое сложение “или” (Выражение Lor) | Логическое умножение “и” (Выражение Land) |
| 
|
| TRUEÞ (-1, 1); FALSE Þ (-0.5, -1) | TRUE Þ (0.5, 1); FALSE Þ (1, -1) |
Варианты заданий
| № | Неравенство A | Неравенство B | Неравенство C | Дополнительная логическая формула |
| x £ 0 | y > 0 | y > x 2 + 2 |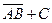 
| |
| x > 0 | y £ 0 | x 2 + y 2< 1 |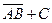
| |
| x > 0 | y > 0 |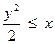 
|
| |
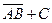
| x £ 0 | y > 0 | x 2 + y 2£ 1 |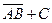
| |
| x £ 0 | y > 0 | y > x 2 – 2 |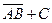
| |
| x £ 0 | y > 0 | y > - x 2 + 2 |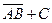
| |
| x £ 0 | y > 0 |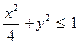 
|
| |
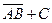
| x > 0 | y > 0 |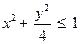 
|
| |
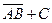
| x £ 0 | y > 0 |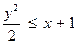 
|
| |
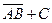
| x > 0 | y > 0 | y £ x 2 – 2 |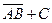
| |
| x £ 0 | y £ 0 | y £ - x 2 + 2 |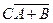 
| |
| x > 0 | y £ 0 |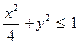
|
| |
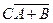
| x > 0 | y £ 0 |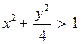 
|
| |
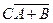
| x > 0 | y > 0 |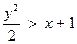 
|
| |
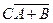
| x £ 0 | y £ 0 | x 2 + y 2> 1 |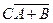
| |
| x > 0 | y > 0 | y > x 2 – 2 |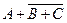 
| |
| x £ 0 | y £ 0 | y £ - x 2 – 2 |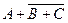 
| |
| x > 0 | y > 0 | y > - x 2 + 2 |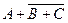
| |
| x > 0 | y £ 0 |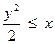
|
| |
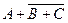
| x > 0 | y > 0 | x 2 + y 2> 1 |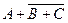
| |
| x > 0 | y £ 0 | y > x 2 – 2 |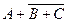 
| |
| x > 0 | y > 0 | y £ - x 2 + 2 |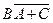 
| |
| x > 0 | y > 0 |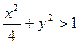 
|
| |
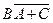
| x £ 0 | y £ 0 |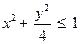
|
| |
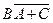
| x > 0 | y £ 0 |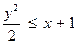
|
| |
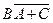
| x > 0 | y £ 0 | y £ x 2 – 2 |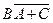
| |
| x > 0 | y £ 0 | y > - x 2 + 2 |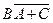
| |
| x £ 0 | y £ 0 |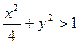
|
| |
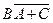
| x £ 0 | y > 0 |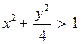
| 
| |
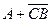
| x £ 0 | y £ 0 |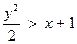
|
| |
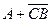
| x > 0 | y > 0 | y > x 2 + 2 |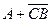
| |
| x > 0 | y £ 0 | y £ - x 2 – 2 |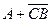
| |
Примечание: CB – логическое произведение с общей инверсией
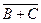– логическая сумма с общей инверсией
Используйте в среде Windows русский пакет aGrapher, чтобы проверить правильность рисования областей.