
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическое занятие.
|
|
Тема. Квадратичные формы. Приведение к каноническому виду методом Лагранжа. Положительно и отрицательно определённые квадратичные формы. Критерии знакоопределённости квадратичных форм.
Квадратичной формой  (кратко
(кратко  ) от
) от 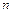 -переменных называется однородный многочлен второй степени:
-переменных называется однородный многочлен второй степени: 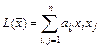 , где
, где 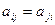 . Квадратичную форму всегда можно записать в матричном виде:
. Квадратичную форму всегда можно записать в матричном виде: 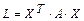 , где
, где  - матрица квадратичной формы (являющаяся симметрической, так как выполняется условие
- матрица квадратичной формы (являющаяся симметрической, так как выполняется условие 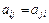 ),
),  - матрица-столбец,
- матрица-столбец, 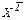 - матрица-строка, составленные из переменных
- матрица-строка, составленные из переменных 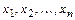 .
.
Квадратичная форма называется невырожденной, если её матрица - невырожденная. Квадратичная форма называется канонической, если она имеет вид: 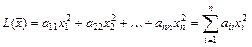 .
.
Всякую квадратичную форму всегда можно привести к канонической, например, методами Лагранжа и ортогональных преобразований.
Метод Лагранжа состоит в последовательном выделении в квадратичной форме полных квадратов. Если в квадратичной форме все коэффициенты  (
(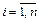 ), а коэффициент
), а коэффициент 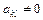 (
(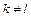 ), то, до выделения полных квадратов, в квадратичной форме следует перейти к новым переменным по формулам:
), то, до выделения полных квадратов, в квадратичной форме следует перейти к новым переменным по формулам:  .
.
Метод ортогональных преобразований состоит в приведении формы 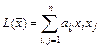 к каноническому виду
к каноническому виду 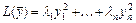 , где
, где 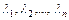 - собственные числа матрицы квадратичной формы. Такое приведение осуществляется с помощью ортогонального преобразования
- собственные числа матрицы квадратичной формы. Такое приведение осуществляется с помощью ортогонального преобразования 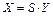 , где
, где 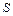 - ортогональная матрица, столбцами которой служат ортонормированные собственные векторы матрицы квадратичной формы;
- ортогональная матрица, столбцами которой служат ортонормированные собственные векторы матрицы квадратичной формы; 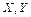 - матрицы-столбцы переменных квадратичной формы.
- матрицы-столбцы переменных квадратичной формы.
Квадратичные формы подразделяют на различные типы в зависимости от множества их значений. Квадратичная форма 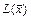 называется: положительно (отрицательно) определённой, если для любого
называется: положительно (отрицательно) определённой, если для любого  выполняется неравенство
выполняется неравенство 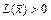 (
(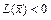 ); неотрицательно (неположительно) определённой, если для любого
); неотрицательно (неположительно) определённой, если для любого 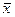 выполняется неравенство
выполняется неравенство 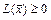 (
(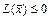 ), причём существует
), причём существует  , для которого
, для которого 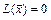 ; знакопеременной (или неопределённой), если существуют такие
; знакопеременной (или неопределённой), если существуют такие 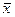 и
и 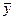 , что
, что 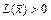 и
и 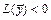 .
.
Невырожденная квадратичная форма может быть либо положительно определённой, либо отрицательно определённой, либо знакопеременной. Тип невырожденной квадратичной формы можно определить, проверяя знаки главных миноров матрицы квадратичной формы. Пусть 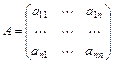 , где
, где 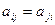 - матрица квадратичной формы. Главными минорами матрицы
- матрица квадратичной формы. Главными минорами матрицы  называются миноры порядка
называются миноры порядка  (
( ), составленные из первых
), составленные из первых 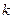 строк и первых
строк и первых 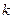 столбцов матрицы:
столбцов матрицы:  ,
, 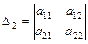 , …,
, …, 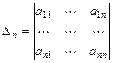 .
.
Одним из критериев знакоопределённости невырожденной квадратичной формы является критерий Сильвестра:
- квадратичная форма 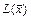 положительно определена тогда и только тогда, когда все главные миноры её матрицы положительны, т.е.
положительно определена тогда и только тогда, когда все главные миноры её матрицы положительны, т.е. 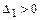 ,
, 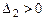 ,
,  ,
, 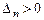 ;
;
- квадратичная форма 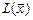 отрицательно определена тогда и только тогда, когда для всех главных миноров её матрицы выполняются неравенства:
отрицательно определена тогда и только тогда, когда для всех главных миноров её матрицы выполняются неравенства: 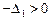 ,
,  ,
,  ,
,  ,
, 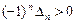 (все миноры нечётного порядка отрицательны, а чётного – положительны);
(все миноры нечётного порядка отрицательны, а чётного – положительны);
- квадратичная форма 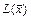 знакопеременна тогда и только тогда, когда для главных миноров её матрицы выполняется хотя бы одно из условий: один из главных миноров равен нулю, один из главных миноров чётного порядка отрицателен, два главных минора нечётного порядка имеют разные знаки.
знакопеременна тогда и только тогда, когда для главных миноров её матрицы выполняется хотя бы одно из условий: один из главных миноров равен нулю, один из главных миноров чётного порядка отрицателен, два главных минора нечётного порядка имеют разные знаки.
1.167 Записать матрицу следующих квадратичных форм:
а) 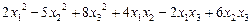 ; б)
; б)  ;
;
в) 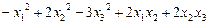 ; г)
; г) 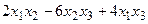 .
.
В задачах 1.168-1.173 методом Лагранжа найти: а) канонический вид квадратичной формы; б) невырожденное линейное преобразование, приводящее к этому виду.
1.168. 1.169.
1.170. 1.171.
1.172. 1.173.
В задачах 1.174-1.179 найти канонический вид квадратичной формы согласно метода ортогональных преобразований.
1.174. 1.175.
1.176. 1.177.
1.178. 1.179.
В задачах 1.180-1.185 определить, используя критерий Сильвестра, какие квадратичные формы являются либо положительно, либо отрицательно определенными, а какие нет.
1.180. 1.181.
1.182. 1.183.
1.184. 1.185.
1.186 Найти, используя критерий Сильвестра, все значения параметра 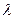 , при которых квадратичная форма является положительно определенной:
, при которых квадратичная форма является положительно определенной:
а)  ; б)
; б) 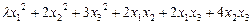 ;
;
В); г).
1.187 Найти, используя критерий Сильвестра, все значения параметра 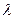 , при которых квадратичная форма является отрицательно определенной:
, при которых квадратичная форма является отрицательно определенной:
а) 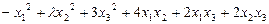 ; б)
; б) 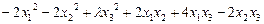 ;
;
В); г).
Ответы: 1.167а)  б)
б) 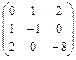 в)
в) 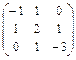 г)
г) 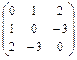
1.168 а) 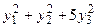 , б)
, б) 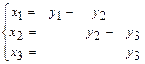 1.169 а)
1.169 а) 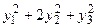 , б)
, б) 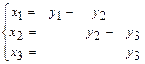
1.170 а)  , б)
, б) 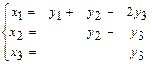 1.171 а)
1.171 а) 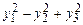 , б)
, б) 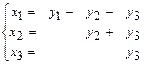
1.172 а) 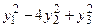 , б)
, б)  1.173 а)
1.173 а) 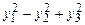 , б)
, б) 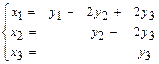
1.174. 1.175. 1.176. 1.177.
Положительноопределенная.1.181Отрицательно определённая. 1.182Общего вида. 1.183Отрицательно определенная. 1.184Положительно определенная. 1.185Положительно определённая. 1.186 а); б); в); г)таких не существует. 1.187 а)Такихне существует; б); в); г).
|