
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Способы измерения расстояний между векторами признаков
|
|
В качестве исходных данных мы имеем усредненные значения параметров для каждого из классов изображений, в процессе работы вычисляются параметры загруженного изображения. Для реализации метода потенциальных функций необходимо каким-либо образом измерять расстояние между векторами признаков, вычисленных для загруженного изображения и заданных в качестве исходных данных.
Если рассматривать образы как элементы метрического пространства, то в качестве функции расстояния можно использовать метрику этого пространства, т.е. такую неотрицательную функцию 
 , которая удовлетворяет условиям (аксиомам метрики):
, которая удовлетворяет условиям (аксиомам метрики):
1) 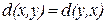 (симметричность);
(симметричность);
2)  ;
;
3) 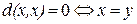 (определенность);
(определенность);
4)  (неравенство треугольника).
(неравенство треугольника).
Пространство 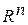 с введенной метрикой называют метрическим пространством. Чаще всего используют следующие метрики:
с введенной метрикой называют метрическим пространством. Чаще всего используют следующие метрики:
· метрика Евклида  ;
;
· манхаттоновская метрика  ;
;
· метрика Канберра  .
.
Выбор метрики в пространстве объектов X является серьёзной проблемой в задачах классификации, кластеризации и непараметрической регрессии. Метрика это математическая модель сходства объектов, и её выбор во многих случаях не однозначен. В то же время, в большинстве метрических алгоритмов предполагается, что метрика фиксирована. В последнее время всё чаще применяются методы, в которых метрика настраивается по обучающей выборке.
Метрика Евклида, используемая для определения расстояния между точками пространства признаков 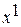 и
и 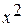 , удовлетворяет всем аксиомам расстояния; она удобна для определения расстояния между двумя точками, например между точкой наблюдаемых параметров и центром класса. Она не учитывает распределение точек в классе. Метрика Евклида позволяет не учитывать знаковые различия, пропорционально увеличивает расстояние между объектами в случае разных абсолютных значений показателей.
, удовлетворяет всем аксиомам расстояния; она удобна для определения расстояния между двумя точками, например между точкой наблюдаемых параметров и центром класса. Она не учитывает распределение точек в классе. Метрика Евклида позволяет не учитывать знаковые различия, пропорционально увеличивает расстояние между объектами в случае разных абсолютных значений показателей.
Второй по значимости функцией расстояния принято считать метрику несхожести или манхаттоновскую метрику, которую при рассмотрении на множестве биполярных векторов 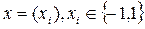 называют метрикой Хемминга. Манаттоновскую метрику можно использоваться в тех случаях, когда знаковые различия характеристик объектов имеют принципиальное значение.
называют метрикой Хемминга. Манаттоновскую метрику можно использоваться в тех случаях, когда знаковые различия характеристик объектов имеют принципиальное значение.
Исследования показали, что евклидово расстояние эффективно при исследованиях слабо коррелированных (шарообразных) совокупностей объектов, а манхеттенское - если объекты образуют плоские вытянутые классы, ортогональные каким-либо координатным осям пространства признаков. Поэтому обработка одной и той же таблицы " объекты-свойства" одним и тем же методом или алгоритмом, но с использованием различных метрик может давать различные, порой кардинально противоположные результаты.
На рисунке 1.5 приведен пример, иллюстрирующий результаты классификации объектов в зависимости от применяемой метрики.
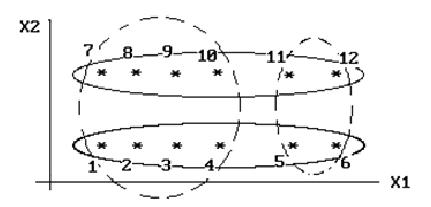
Рисунок 1.5 - Зависимость результатов классификации от типа используемой метрики
При использовании манхеттенского расстояния образуются классы, вытянутые вдоль оси абсцисс (обозначены на рисунке 1.5 сплошными линиями), а при использовании евклидового расстояния объекты группируются в два более или менее компактных класса (обозначены рисунке 1.5 пунктирными линиями). Из этого следует, что к выбору метрики следует подходить весьма продуманно и осторожно, сопоставляя результаты использования различных метрик между собой и с целями предпринятой обработки эмпирических данных.
Заметим, что метрика Канберра, в отличие от ранее рассмотренных метрик, является неинвариантной относительно сдвига векторов.