Минимаксный критерий

Задача ставится следующим образом: из всех возможных наборов при условиях 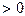и 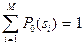необходимо выбрать такой (и в дальнейшем его использовать при распознавании), при котором максимальная компонента вектора 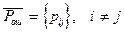, минимальна.

Алгоритмически одним из наиболее простых является метод Монте-Карло. Случайным образом 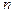раз выбираются векторы Тот вектор, при котором максимальная компонента 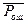принимает наименьшее значение, принимается для использования. Чем больше 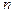, тем выше вероятность " попадания" в ближайшую окрестность оптимального вектора . Возможен, конечно, и полный перебор вариантов, но он приемлем лишь при не очень большом числе возможных . В некоторых частных задачах может быть реализован аналитический подход к поиску . Рассмотрим случай с двумя образами (рис. 21).

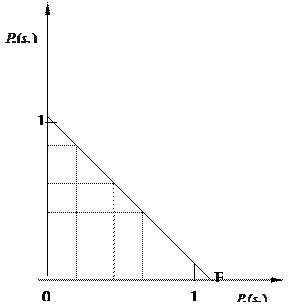
Рис. 21. Область решения задачи определения
по минимаксному критерию

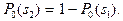Решение минимаксной задачи лежит на отрезке прямой Обозначим через область объектов первого образа, а через – второго. Ясно, что При этом средняя вероятность ошибок распознавания определяется величиной 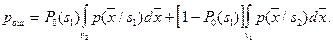Построим график (рис. 22).

Очевидно, что 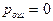при и =1. Между ними находятся значения , при которых , в том числе максимальное её значение. Допустим, что мы выбрали = . Тогда 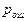как функция истинного (но неизвестного) значения лежит на прямой, касательной к в точке, соответствующей = . При этом если истинное значение лежит левее точки (например, = ), то фактическая средняя ошибка распознавания (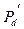) окажется меньше, чем прогнозируемая при = . Зато если истинное значение = , то фактическая средняя ошибка (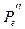) окажется существенно больше прогнозируемой. Аналогичные рассуждения можно привести и для правого склона кривой , положив, например, = . 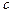Лишь выбрав = 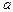, что соответствует максимуму кривой , мы гарантируем, что не превзойдёт , каково бы ни было истинное значение .

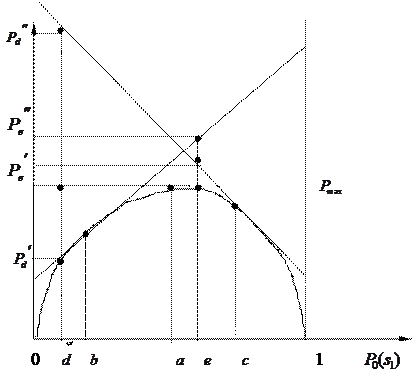Рис. 22. Зависимость вероятности ошибки распознавания
от

Рассмотрим аналитическую постановку задачи поиска минимаксного решения (при этом следует иметь в виду, что 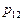и зависят от , поскольку они есть функции от и , а последние зависят от априорных вероятностей образов).

Обозначим через . Необходимо найти такое значение , при котором

где .

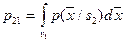Из этого уравнения видно, что найти аналитическое его решение весьма непросто. Во-первых, необходимо записать в явном виде зависимость 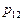и от , а во-вторых, уравнение должно иметь аналитическое решение. В простейших случаях это возможно, но простейшие случаи, к сожалению, крайне редко встречаются на практике.