
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аннуитеты.
|
|
Поток однонаправленных платежей с равными интервалами между последовательными платежами в течение определенного количества лет называется аннуитетом (финансовой рентой).
Теория аннуитетов является важнейшей частью финансовой математики. Она применяется при рассмотрении вопросов доходности ценных бумаг, в инвестиционном анализе и т. д. Наиболее распространенные примеры аннуитета: регулярные взносы в пенсионный фонд, погашение долгосрочного кредита, выплата процентов по ценным бумагам.
Аннуитеты различаются между собой следующими основными характеристиками:
· величиной каждого отдельного платежа;
· интервалом времени между двумя последовательными платежами (периодом аннуитета);
· сроком от начала аннуитета до конца его последнего периода (бывают и неограниченные по времени — вечные аннуитеты);
· процентной ставкой, применяемой при наращении или дисконтировании платежей.
Аннуитет, для которого платежи осуществляются в начале соответствующих интервалов, носит название аннуитета пренумерандо; если же платежи осуществляются в конце интервалов, мы получаем аннуитет постнумерандо (обыкновенный аннуитет) —пожалуй, самый распространенный случай.
Наибольший интерес с практической точки зрения представляют аннуитеты, в которых все платежи равны между собой (постоянные аннуитеты), либо изменяются в соответствии с некоторой закономерностью.
Введем следующие обозначения:
Ø Рк — величина каждого отдельного платежа;
Ø iс — сложная процентная ставка, по которой начисляются
проценты;
Ø Sk — наращенная сумма для k-то платежа аннуитета постну-
мерандо;
Ø Sан. — наращенная (будущая) сумма всего аннуитета постнумерандо (т. е. сумма всех платежей с процентами);
Ø Ak — современная величина k-го платежа аннуитета постну-
мерандо;
Ø А — современная величина всего аннуитета постнумерандо
(т. е. сумма современных величин всех платежей);
Ø Sп — наращенная сумма аннуитета пренумерандо;
Ø Aп — современная величина аннуитета пренумерандо;
Ø nn — число платежей.
Будущая стоимость аннуитета постнумерандо
Сумма Sан. 1 для первого платежа, проценты на который будут начисляться, очевидно, (пn — 1) раз, составит по формуле (3.1): 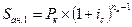 .
.
Для второго платежа (проценты на него будут начисляться на один год меньше) имеем: 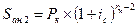 и так далее. На последний платеж, произведенный в конце /1-го года, проценты уже не начисляются, т. е.
и так далее. На последний платеж, произведенный в конце /1-го года, проценты уже не начисляются, т. е.  .
.
Тогда для общей наращенной суммы имеем:
| 7.1 | 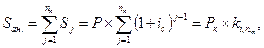
|
Где
Ø ki, nn — коэффициент наращения аннуитета с параметрами i,
Ø пn — представляет собой, как можно заметить, сумму членов гео-
метрической прогрессии, для которой первый член а 1 равен 1, а знаменатель (назовем его q) составляет (1 + ic).
Используя математическую формулу для суммы членов геометрической прогрессии: 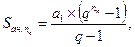
запишем выражение (7.1) в более удобном для вычислений виде:
| 7.2 | 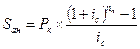 . .
|
Для коэффициента наращения, соответственно, имеем:
| 7.3 | 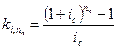 . .
|
Современная величина аннуитета постнумерандо
При заданной процентной ставке ic современное значение каждого платежа будет определяться по формуле: 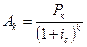 .
.
Современная величина всего аннуитета, следовательно, составит: 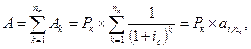
где ai, n — коэффициент приведения аннуитета, опять является суммой геометрической прогрессии, теперь уже с параметрами a1 = q = 1/(1 + ic).
Тогда для ai, n получаем выражение:
| 7.4 | 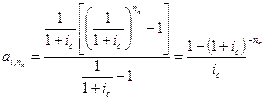
|
для современной величины А соответственно:
| 7.5 | 
|
Как видим, современная величина и наращенная сумма аннуитета связаны между собой соотношением:
| 7.6 | 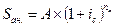 . .
|
Из полученных формул путем преобразований легко получить еще несколько формул. Так, для определения размера очередного платежа (Р) имеем:
| 7.7 |  , ,
|
| 7.8 | 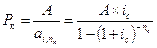 . .
|
Для определения срока аннуитета (n), при прочих заданных условиях, получаем:
| 7.9 | 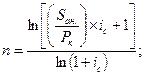
|
| 7.10 | 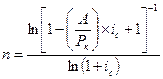 . .
|
Для конкретных вычислений выбирается одна из двух формул каждой пары в зависимости от заданных известных величин.
Будущая стоимость аннуитета пренумерандо
| 7.11 | 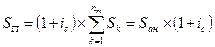 . .
|
Для коэффициента наращения аннуитета пренумерандо ki, n получаем следующее соотношение:
| 7.12 | 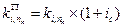 . .
|
Можно также заметить, что для определения современных значений каждого платежа дисконтирование по заданной ставке ic проводится на один раз меньше, чем в случае аннуитета пренумерандо. Поэтому каждая современная величина Аk будет больше в (1 + i) раз. Таким образом,
| 7.13 | 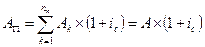 . .
|
А для коэффициента приведения ai, n получаем:
| 7.14 | 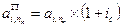 . .
|
Для нахождения размера платежа и срока аннуитета пренумерандо можно по формулам (7.11) и (7.13) найти для заданных значений S п и A п соответствующие значения S и A и пользоваться далее формулами, выведенными для аннуитета постнумерандо.
Для определения коэффициентов наращения и приведения обыкновенного аннуитета существуют таблицы, которыми удобно пользоваться в практических вычислениях. Максимальные процентные ставки в таких таблицах обычно не превышают 30-40%, что значительно ниже размера процентных ставок, применяемых в России в настоящее время. Но нужно иметь в виду, что п в данном случае — не число лет, а число периодов одинаковой продолжительности (день, месяц, квартал и т.д.), в которых принята данная процентная ставка. Таким образом, если задана годовая процентная ставка, можно найти эквивалентную ей ставку на более коротком интервале и рассматривать далее n как число таких интервалов.
Если срок аннуитета п не ограничен, мы получаем случай вечного аннуитета. Для аннуитета постнумерандо выражения для наращенной суммы и современной величины приобретут следующий вид:
| 7.15 | 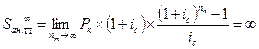 , ,
|
| 7.16 | 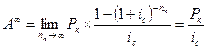 . .
|
Для аннуитета пренумерандо, соответственно, получаем:
| 7.17 | 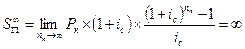 , ,
|
| 7.18 | 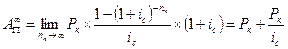 . .
|
Таким образом, различие между двумя типами вечных аннуитетов, естественно, сказывается на определении их современной величины.
Не менее важен случай, когда последовательность платежей изменяется по некоторому закону, и, следовательно, также может быть описана с помощью математических средств.
Рассмотрим обыкновенный аннуитет, в котором платежи постоянно увеличиваются на определенную положительную величину h, т. е. являются членами арифметической прогрессии с первым членом а 1 = Р и разностью h. Т. е. платежи представляют собой ряд: Р, Р+ h, P + 2h,...Р+ (п- 1 )*h.
Для наращенной суммы всего аннуитета получаем следующее выражение:
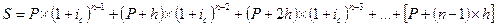 .
.
Умножим обе части данного равенства на (1 +ic) и вычтем первое выражение из полученного после умножения:
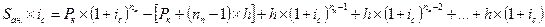 .
.
Видно, что часть полученного равенства представляет собой сумму членов геометрической прогрессии, где a 1= h*( 1 + ic), q = (I + ic). После несложных преобразований получаем:
| 7.19 | 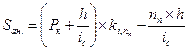 . .
|
Используя формулу (7.6), находим современное значение аннуитета:
| 7.20 | 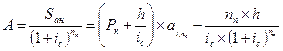 . .
|
Возможен также случай, когда платежи постоянно возрастают в q раз, т. е.
являются членами геометрической прогрессии: 
Тогда для наращенной суммы аннуитета имеем:
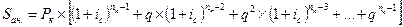 .
.
В квадратных скобках мы получили геометрическую прогрессию с первым членом a1 = (1+ ic) и знаменателем q/( 1 + ic). Используя опять формулу для суммы геометрической прогрессии, получаем выражение для S:
 .
.
По формуле (7.6) находим современное значение А:
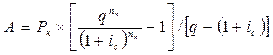 .
.
Складывая получившиеся величины, находим современную величину всего потока платежей: А =А 1 + a2 + А3 + А 4 = 2657, 94 ам. долл.
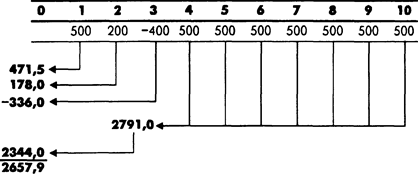
Современная величина аннуитета.
Во всех случаях, когда в произвольном потоке платежей встречаются серии, которые могут быть описаны как постоянные или изменяющиеся по некоторому закону аннуитеты, следует обращать внимание на начальный момент и срок этих аннуитетов, не совпадающие с начальным моментом и сроком полного потока платежей.
Следующий этап нашего изучения — конверсия аннуитетов. Под конверсией аннуитета понимается такое изменение начальных параметров аннуитета, после которого новый аннуитет был бы эквивалентен данному.
Два аннуитета считаются эквивалентными, если равны их современные величины, приведенные к одному и тому же моменту времени.
|