
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Действия с дискретными случайными величинами
|
|
Действия со случайными величинами. Свойства математического ожидания и дисперсии
Действия с дискретными случайными величинами
Суммой двух дискретных случайных величин Х и Y называется случайная величина Z, которая принимает все возможные значения вида 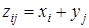 с соответствующими вероятностями
с соответствующими вероятностями 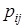 .
.
Разностью 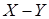 называется случайная величина Z, принимающая все возможные значения вида
называется случайная величина Z, принимающая все возможные значения вида 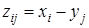 с соответствующими вероятностями
с соответствующими вероятностями 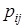 .
.
Произведением 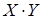 называется случайная величина Z, которая принимает все возможные значения вида
называется случайная величина Z, которая принимает все возможные значения вида 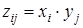 с соответствующими вероятностями
с соответствующими вероятностями 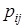 .
.
Под 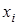 понимается любое из значений случайной величины Х:
понимается любое из значений случайной величины Х: 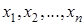 , а под
, а под 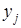 любое из значений случайной величины Y:
любое из значений случайной величины Y: 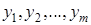 . Способ вычисления вероятности
. Способ вычисления вероятности 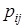 определяется тем, какого рода случайные величины участвуют в действии. Если эти величины независимы, т.е. вероятность того, что Х примет некоторое значение х, не зависит от того, какое значение примет Y, то
определяется тем, какого рода случайные величины участвуют в действии. Если эти величины независимы, т.е. вероятность того, что Х примет некоторое значение х, не зависит от того, какое значение примет Y, то
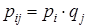 , где
, где 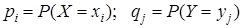 .
.
Если величины Х и Y зависимы, то используются условные вероятности.
Выполнение действий с двумя случайными величинами удобно вести следующим образом.
Пример. Даны две независимые случайные величины Х и Y:
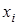
| – 2 | 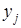
| ||||||||
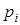
| 0, 1 | 0, 2 | 0, 2 | 0, 3 | 0, 2 | 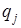
| 0, 3 | 0, 3 | 0, 4 |
Найти ряд распределения случайной величины 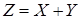 . Значения величины Z и их вероятности найдем с помощью таблицы. В клетках этой таблицы вверху слева указаны значения Z при соответствующих значениях Х и Y, внизу справа указаны их вероятности.
. Значения величины Z и их вероятности найдем с помощью таблицы. В клетках этой таблицы вверху слева указаны значения Z при соответствующих значениях Х и Y, внизу справа указаны их вероятности.
| Х | –2 | |||||||||||
| Y | 0, 1 | 0, 2 | 0, 2 | 0, 3 | 0, 2 | |||||||
| 0, 3 | ||||||||||||
| 0, 03 | 0, 06 | 0, 06 | 0, 09 | 0, 06 | ||||||||
| 0, 3 | ||||||||||||
| 0, 03 | 0, 06 | 0, 06 | 0, 09 | 0, 06 | ||||||||
| 0, 4 | ||||||||||||
| 0, 04 | 0, 08 | 0, 04 | 0, 12 | 0, 09 | ||||||||
Выпишем ряд распределения Z:

| |||||||||||||||
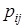
| 0, 03 | 0, 06 | 0, 06 | 0, 03 | 0, 09 | 0, 06 | 0, 06 | 0, 06 | 0, 04 | 0, 09 | 0, 08 | 0, 06 | 0, 08 | 0, 12 | 0, 06 |
Следует отметить некоторые отличия действий со случайными величинами от действий с обычными величинами, например, 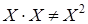 . Определим
. Определим 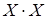 :
:
| X | –2 | ||||||||||
| X | 0, 1 | 0, 2 | 0, 2 | 0, 3 | 0, 2 | ||||||
| –2 | 0, 1 | –4 | –8 | –12 | |||||||
| 0, 01 | 0, 02 | 0, 02 | 0, 03 | 0, 02 | |||||||
| 0, 2 | |||||||||||
| 0, 02 | 0, 04 | 0, 04 | 0, 06 | 0, 04 | |||||||
| 0, 2 | –4 | ||||||||||
| 0, 02 | 0, 04 | 0, 04 | 0, 06 | 0, 04 | |||||||
| 0, 3 | –8 | ||||||||||
| 0, 03 | 0, 06 | 0, 06 | 0, 09 | 0, 06 | |||||||
| 0, 2 | –12 | ||||||||||
| 0, 02 | 0, 04 | 0, 04 | 0, 06 | 0, 04 |
В ряд распределения 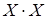 повторяющиеся значения заносим с суммарной вероятностью
повторяющиеся значения заносим с суммарной вероятностью
| –12 | –8 | –4 | |||||||
| 0, 04 | 0, 06 | 0, 04 | 0, 36 | 0, 05 | 0, 12 | 0, 08 | 0, 09 | 0, 12 | 0, 04 |
Распределение же 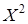 выглядит так
выглядит так
| 0, 2 | 0, 3 | 0, 3 | 0, 2 |
Если в действии участвуют более двух случайных величин, то действие можно выполнить последовательно. Например, чтобы найти сумму 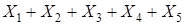 , нужно найти
, нужно найти 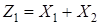 ,
, 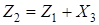 ,
, 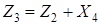 ,
, 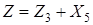 .
.
Действия с непрерывными случайными величинами определить гораздо сложнее, кроме того, практически в опыте непрерывные случайные величины представлены набором дискретных значений, поэтому действия с непрерывными случайными величинами рассматривать не будем.
Во многих случаях вполне достаточно бывает, не выписывая подробно распределения случайной величины, полученной в результате действий с другими случайными величинами, найти ее числовые характеристики.