
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства числовых характеристик случайной величины
|
|
Первые два свойства легко получаются из определения математического ожидания.
1. Математическое ожидание постоянной величины равно этой постоянной.
2. Постоянный множитель можно выносить за знак математического ожидания
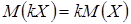
3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий.
Возьмем для примера случайные величины X и Y, заданные следующим образом
| X: | x 1 | x 2 | Y: | y 1 | y 2 | y 3 |
| p 1 | p 2 | q 1 | q 2 | q 3 |
Используя определение суммы случайных величин и математического ожидания, можем написать
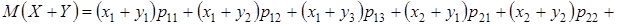
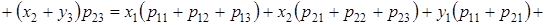
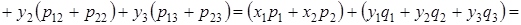
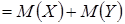
Это свойство можно распространить на сумму любого конечного числа случайных величин
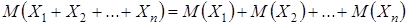 .
.
4. Математическое ожидание разности случайных величин равно разности их математических ожиданий
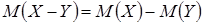 .
.
5. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий
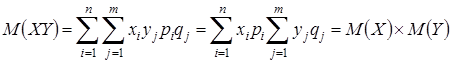 .
.
6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно 0. Используя свойства 1 и 4, получим
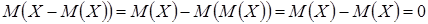 .
.
Теперь рассмотрим свойства дисперсии, предварительно вспомнив ее определение. Дисперсия случайной величины X равна математическому ожиданию квадрата отклонения X от M (X):
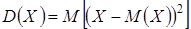 .
.
7. Дисперсия постоянной величины равна 0.
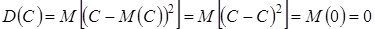 .
.
8. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
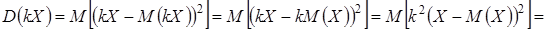
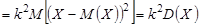 .
.
9. Дисперсия суммы случайных величин равна сумме дисперсий этих величин плюс удвоенный коэффициент ковариации.
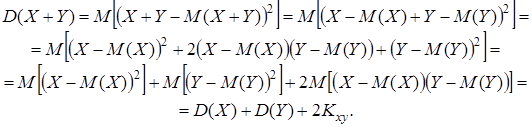
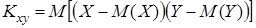 – корреляционный момент, также называемый коэффициентом ковариации, т.е. коэффициентом совместного изменения. Коэффициент ковариации можно преобразовать следующим образом:
– корреляционный момент, также называемый коэффициентом ковариации, т.е. коэффициентом совместного изменения. Коэффициент ковариации можно преобразовать следующим образом:
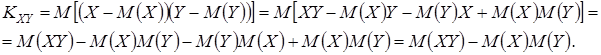
Если случайные величины Х и Y независимы, то дисперсия их суммы равна сумме дисперсий: 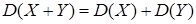 . Действительно, если Х и Y независимы, то и их отклонения от математических ожиданий будут независимы. Используя свойства 5 и 6,
. Действительно, если Х и Y независимы, то и их отклонения от математических ожиданий будут независимы. Используя свойства 5 и 6,
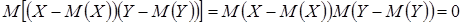 .
.
В этом случае 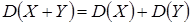 . Дисперсия суммы независимых случайных величин равна сумме их дисперсий
. Дисперсия суммы независимых случайных величин равна сумме их дисперсий
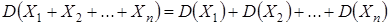 .
.
10. Дисперсия разности независимых случайных величин равна сумме их дисперсий
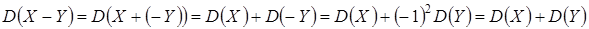 .
.