
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Энтропия как мера информации.
|
|
Технологический процесс, протекающий под управлением АСУТП, сопровождается информационными процессами, протекающими внутри АСУТП. Информационные процессы включают в себя:
• приём и запоминание управляющих программ;
• приём и запоминание текущей информации о параметрах техпроцесса и параметрах АСУТП;
• формирование управляющих сигналов, воздействующих на управляемый техпроцесс, и передачу их по каналам УСО;
• формирование информации о ходе техпроцесса и состоянии АСУТП для верхнего уровня управления с целью передачи её по запросам ЦУВМ или оператора.
С точки зрения информационных процессов рассмотрим техпроцесс и управляющие им сигналы как последовательность запланированных (предусмотренных) событий. События – это факты реализуемого производственного процесса. Реализованное событие называют исходом. Описание происходящих событий называют сообщениями. Все рассматриваемые сообщения – дискретные величины, начиная с сигналов на включение и отключение какого-либо оборудования и вплоть до показаний стрелочных измерительных приборов, дискретность которых определяется ценой деления шкалы. Информацией называется процесс формирования, пересылки и регистрации (запоминания) сообщений, а также зарегистрированная совокупность сообщений.
Смысл сообщений, содержательная сторона информации, определяется известными закономерностями хода событий. Будем рассматривать не смысл, а количественную оценку информации, объём записей, которые необходимо сделать для регистрации сообщений. Объём записей существенно зависит от совокупности символов, применяемых для записи информации. Такая совокупность обычно имеет вид основания системы исчисления или алфавита. Если в качестве основания используется совокупность n символов, то с её помощью можно сформировать не более чем 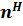 различных сообщений об интересующих нас событиях. Тогда величину H можно определить из соотношения:
различных сообщений об интересующих нас событиях. Тогда величину H можно определить из соотношения:
 , (2.1)
, (2.1)
где M – число возможных вариантов события, сообщения о котором нам необходимо сформировать в зависимости от того, какой вариант состоится.
Величину H, равную числу элементов сообщения и характеризующую минимальный объём сообщения о том, что один из интересующих нас M вариантов изучаемого процесса действительно имел место, принято называть энтропией.
Если при планировании техпроцесса предполагается, что его результат однозначно предопределён, что исход будет однозначным, то в формуле (2.1) примем M = 1 и получим H = 0. Однако однозначный результат гарантировать невозможно. Исход техпроцесса и даже его простейших операций зависит от множества случайных факторов, действие которых оценивают методами теории вероятности. Так, если все предполагаемые события равновероятны и образуют полную группу (т.е. при каждом повторении изучаемого процесса происходит хотя бы одно из них), то вероятность P каждого из этих событий определяется по формуле:
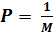 ,
,
и соотношение (2.1) можно записать в виде:
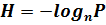 . (2.2)
. (2.2)
Здесь величина H выступает как мера априорной неопределённости любого из исходов изучаемого процесса. Чем меньше вероятность P (чем больше вариантов равновероятных исходов), тем больше энтропия процесса. Таким образом, энтропия может быть использована для оценки степени случайности техпроцесса или какой-либо из технологических операций как мера неупорядоченности процесса. Обычно изучаемые события не равновероятны, характеризуются вероятностями 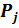 и их энтропия рассчитывается по формуле Шеннона:
и их энтропия рассчитывается по формуле Шеннона:
 , (2.3)
, (2.3)
Причём необходимо, чтобы изучаемые события составляли полную группу, когда:
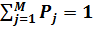 .
.
Величина H, рассчитанная по формуле (2.3), является математическим ожиданием, т.е. средним значением минимального объёма записей, которые необходимо сделать для фиксирования факта реализации одного из M интересующих нас событий. Запишем  каждого из этих событий в виде соотношения:
каждого из этих событий в виде соотношения:
 ,
,
где 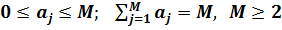 .
.
Подставив данное соотношение в формулу (2.3), получим:
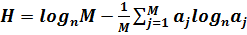 . (2.4)
. (2.4)
Если все рассматриваемые события равновероятны, то все  и с отношения (2.3) и (2.4) сводятся к соотношению (2.1). В остальных случаях величина H будет уменьшена на величину:
и с отношения (2.3) и (2.4) сводятся к соотношению (2.1). В остальных случаях величина H будет уменьшена на величину:
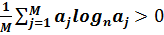 ,
,
т.е. максимальное значение энтропии соответствует равной вероятности событий изучаемого процесса. Величина энтропии как минимального объёма сообщения используется для оценки количества информации. Поскольку фактическое распределение вероятностей исходов чаще всего неизвестно, то при определении объёма запоминающих устройств и пропускной способности каналов связи обычно руководствуются формулой (2.1).