
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многомерные модели.
|
|
До сих пор мы рассматривали идентификацию одномерных объектов, моделируемых функциями одного переменного. Такой подход применим в основном при моделировании отдельных звеньев технологических объектов, но сами ТО являются, как правило, многосвязными, многомерными системами. Модели таких объектов получают посредством факторного анализа, который называют также методом планирования эксперимента. Данный метод базируется на линейной аппроксимации функций исследуемых объектов. Ввиду разброса результатов экспериментальных исследований многомерная линейная модель формируется как линейная регрессия моделируемого выходного параметра y на управляющие (входные) параметры x1, x2, …, xm.
Уравнение линейной регрессии y на x1, x2, …, xm записывают в следующем виде:
 , (3.15)
, (3.15)
где y0, x0 – средние значения y и xi, рассчитанные по формулам (3.10) и (3.11) в заданном диапазоне изменения y и xi;
⋀ yi, ⋀ ii – обобщённый корреляционный момент и обобщённая дисперсия, выраженные в матричной форме.
Факторы x1, x2, …, xm, существенно влияющие на выходной параметр y, обычно представляют в относительных величинах:
 (3.16)
(3.16)
 ,
,
где xi max – максимальное запланированное значение xi.
После подстановки xiэ в уравнение (3.15) получим:
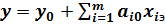 , (3.17)
, (3.17)
где 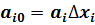 .
.
Задачей факторного анализа является рациональное планирование экспериментальных исследований изучаемого объекта, позволяющее по их результатам наименее трудоёмким путём определить коэффициенты a1, a2, …, am уравнения линейной регрессии (3.15), моделирующего данный объект. Коэффициенты определяются таким образом, чтобы расчётные значения y, полученные по формуле (3.17), были равны экспериментальным значениям y, полученным при тех же значениях xiэ. Если будут проведены n циклов экспериментального определения значений y при различных наборах значений входных параметров (факторов) xi, то для определения параметров ai можно будет составить n уравнений вида:
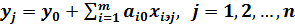 . (3.18)
. (3.18)
где yj – значение y, полученное в j -м эксперименте;
xiэj – относительное значение xi в j -м эксперименте.
В матричной форме эта система уравнений может быть представлена в виде:
 , (3.19)
, (3.19)
где Y – матрица-столбец экспериментальных значений yj – y0 с числом элементов, равным n;
Хэ – матрица входных воздействий размером m x n;
A0 – матрица-столбец коэффициентов ai0 с числом элементов, равным m.
Значения xi при проведении экспериментальных исследований варьируют таким образом, чтобы решение системы уравнений (3.18) относительно коэффициентов ai0 можно было представить в виде:
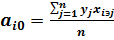 , (3.20)
, (3.20)
где n – число опытов по определению значений yi.
Для этого эксперименты проводят в следующем порядке:
• в каждом эксперименте полагают либо xi = xi max, либо xi = xi min, с тем чтобы всегда получать xiэ = 1 либо xiэ = -1 для всех варьируемых факторов (условие нормированности);
• сумма всех экспериментальных значение каждого фактора xiэ в серии из n экспериментов должна быть равна нулю, т.е. должно выполняться равенство  (условие симметричности);
(условие симметричности);
• сумма всех произведений xiэx(i-1)э в серии из n экспериментов должна быть равна нулю (условие ортогональности).
Значения xi max и xi min выбираются в зависимости от целей линеаризации параметра y. Чем ближе значение xi min к xi max, тем точнее аппроксимация функции y в области значений xi от xi max до xi min, но тем сложнее ограничивать разброс экспериментальных значений параметров в пределах, обеспечивающих заданную точность.
Если следовать рассмотренному порядку экспериментальных исследований, то окажется, что в ходе эксперимента каждый параметр (фактор) будет принимать только два значения: xi max и xi min. Если варьируется m факторов, то максимальное число различных вариантов в одном цикле экспериментальных исследований составит 2m.
Если в экспериментальном цикле реализуются все 2m вариантов, то такой эксперимент называется полнофакторным. Полнофакторный эксперимент всегда удовлетворяет условиям нормированности, симметричности и ортогональности. Он также обеспечивает максимальную точность расчётов. Однако если желательно уменьшить объём эксперимента, то можно применить дробнофакторный эксперимент, когда в цикл экспериментальных исследований входят не все возможные варианты сочетаний факторов, но условия нормированности, симметричности и ортогональности всё же выполняются.
Пример 3.2. Апроксимировать зависимость объёмной производительности J товарного станка от глубины резания tp и подачи на оборот s при постоянной скорости резания уравнением регрессии вида:
 . (3.21)
. (3.21)
| tp, мм |
|
| ||||||||||
| |||||||||||
|
| ||||||||||
|
|
|
|
Рис.3.3. График производительности токарного станка:
1 – J = 200 см3/мин; 2 – J = 250 см3/мин; 3 – J = 300 см3/мин; 4 – J = 350 см3/мин;
5 – J = 400 см3/мин; 6 – J = 450 см3/мин; 7 – J = 500 см3/мин; 8 – J = 550 см3/мин;
9 – J = 600 см3/мин.
Усреднённость кривых tp(s) позволяет предположить:
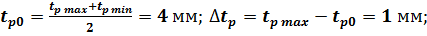
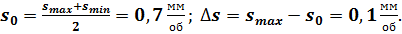
Кроме того, полагаем:
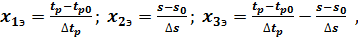
что позволяет искать выражение (3.21) в форме линейной регрессии:
 (3.22)
(3.22)
в соответствии с выражениями (3.17) и (3.18), где полагаем y = J. В рассматриваемом случае m = 3, что ведёт к полнофакторному эксперименту для определения значений a10, a20 и a30 в объёме восьми опытов. С целью уменьшения объёма опытов ограничиваемся четырьмя опытами (n = 4), проведёнными в порядке, указанном в табл.3.2.
Таблица 3.2
Порядок проведения опытов
| Номер опыта | x1э | x2э | x3э | yj= Jj |
| -1 | -1 | |||
| -1 | -1 | |||
| -1 | -1 | |||
Значения x1э и x2э, равны +1 при максимальных значениях tp и s и -1 – при минимальных значениях tp и s. Значения x3э равны произведению значений x1э и x2э. Экспериментальные значения J, соответствующие принятым значениям x1э, x2э и x3э, определены по точкам a, b, d и c на рис.3.3. Как видно из табл.3.2, дробнофакторный эксперимент, отображённый в ней, соответствует требованиям нормированности, симметричности и ортогональности. Поэтому согласно выражению (3.20) вычисляем:

аналогично получаем a20 = 35 и a30 = 7, 5. Кроме того, согласно выражению (3.10) получаем:
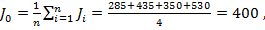
после чего выражение (3.22) будет представлено в виде:
 . (3.23)
. (3.23)
Выражение (3.23) приводится к виду (3.21) в следующей форме:
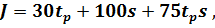
так как a0 = 0.
Получение аналитического выражения J(tp, s) было обеспечено наличием усреднённых экспериментальных зависимостей tp(s), приведённых на рис.3.3. Определение зависимостей такого рода в условиях разброса экспериментальных данных требует применения регрессионного анализа в соответствии с выражениями (3.7) и (3.8), причём необходимо, чтобы объём и число повторений эксперимента обеспечивали нужный уровень достоверности модели.
Приложение 3