
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПЗ.7. Числовые характеристики распределения вероятностей.
|
|
Числовые характеристики распределения случайной величины подразделяются на характеристики положения, определяющие характерные значения случайной величины, и характеристики рассеяния. Из характеристик положения наиболее интересным для нас является среднее значение дискретной случайной величины, формируемое через распределение её вероятностей аналогично среднему арифметическому. Оно задаётся следующим определением: математическим ожиданием (или средним значением) МХ дискретной случайной величины Х называется сумма произведений всех её возможных значений xi на их вероятности pi:
 . (П.3.18)
. (П.3.18)
Аналогично, математическим ожиданием (или средним значением) МХ непрерывной случайной величины Х называется интеграл от произведения её значений х на плотность распределения вероятностей p(x):
 . (П.3.19)
. (П.3.19)
где α, β – соответственно начальное и конечное значения Х на интервале (α, β), на котором сосредоточены все возможные значения величины Х.
Аналогия формул (П.3.18) и (П.3.19) становится очевидной, если принять во внимание, что здесь элемент вероятности p(x)dx аналогичен вероятности pi, а интеграл (П.3.19) – это сумма бесконечно малых слагаемых x*p(x)*dx.
Соответственно математическое ожидание функции Y = f(x) от случайной величины Х выражается через закон распределения самой величины Х:
а) для дискретной величины Х –
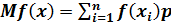 ; (П.3.20)
; (П.3.20)
б) для непрерывной величины Х –
 . (П.3.21)
. (П.3.21)
Математическое ожидание называют также центром распределения случайной величины, так как её рассеяние определяется относительно математического ожидания.
Основные свойства математических ожиданий:
1) постоянный множитель можно выносить за знак математического ожидания:
MCX=CMX;
2) математическое ожидание суммы случайных величин равно сумме их математических ожиданий:
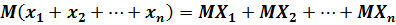 ;
;
3) математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
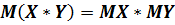 .
.
Важнейшими числовыми характеристиками рассеяния случайной величины являются дисперсия и среднеквадратическое отклонение, определяемое по формуле:
 , (П.3.22)
, (П.3.22)
где a – математическое ожидание (среднее значение) случайной величины Х;
M(X-a)2 – среднее значение квадрата отклонения Х от среднего значения a.
Подкоренное выражение в формуле (П.3.22) часто употребляется самостоятельно, поэтому оно получило название дисперсии случайной величины Х:
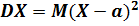 . (П.3.23)
. (П.3.23)
Выражение (П.3.23) можно также записать в виде:
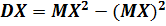 .
.
Согласно соотношению (П.3.20) дисперсия дискретной величины равна:
 , (П.3.24)
, (П.3.24)
а согласно соотношению (П.3.21) дисперсия непрерывной величины равна:
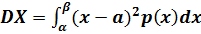 , (П.3.25)
, (П.3.25)
где α и β – крайние точки интервала существования Х.
Основные свойства характеристик рассеяния:
1) у линейной функции случайной величины Х:
 ,
,
дисперсия увеличивается в k2 раз, а среднеквадратическое отклонение – в  раз;
раз;
2) если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий:
 ,
,
соответственно:
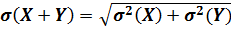 .
.
В частности, дисперсия среднего арифметического n случайных величин, имеющих одинаковую дисперсию, составляет δ 2/n, так что среднеквадратическое отклонение в этом случае равно:
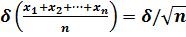 . (П.3.26)
. (П.3.26)
При испытаниях, заключающихся в проверке наличия или отсутствия какого-либо признака и ведущих к биноминальному распределению (см. вопрос П.3.4), наличие признака можно обозначить как х = 1, а его отсутствие – как х = 0. Если вероятность наличия признака равна p, то математическое ожидание при биноминальном распределении окажется равным согласно (П.3.18):
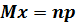 .
.
Обозначив вероятность отсутствия признака через q и исходя из соотношения (П.3.24), получим в случае однократной проверки наличия признака дисперсию:
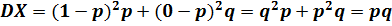 .
.
В общем случае биноминального распределения (когда производится n -кратная выборка) получим:
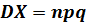 . (П.3.27)
. (П.3.27)
Если имеется простейший поток событий, ведущий к распределению Пуассона (формула П.3.15), то его математическое ожидание можно вывести непосредственно из формулы (П.3.18), полагая, что Х = m, m ≥ 0. Получим:
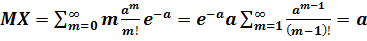 .
.
Если a = λ t при λ = const, то a – это среднее число событий простейшего потока, наступающих за заданное время t и приходящихся на один наблюдаемый объект. Аналогичными рассуждениями можно показать, что дисперсия распределения Пуассона совпадает с его математическим ожиданием:  .
.