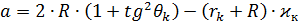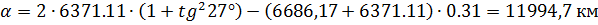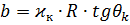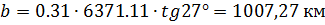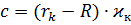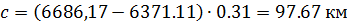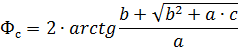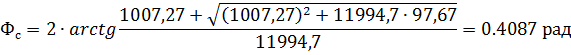Математическая модель движения РКЛА на свободном участке траектории полета. 2.1Принятые допущения и системы координат

2.1Принятые допущения и системы координат

- Земля не вращается Ω _з=0;

- гравитационные поля центральные:

;

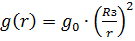- Атмосфера отсутствует;

- Считаем РКЛА материальной точкой.

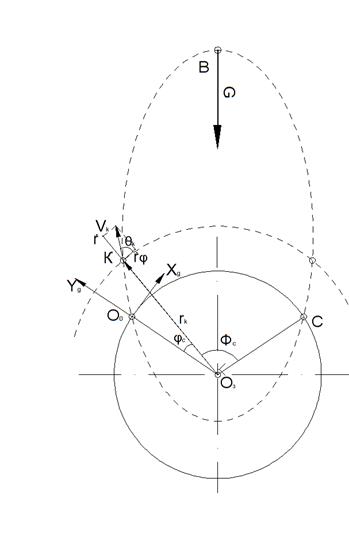
2.2 Схема сил, действующих в полете

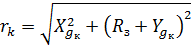
Линейная дальность:

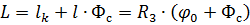
2.3 Для записи уравнений движения ипосльзуем метод Лагранжа. Функция Лагранда представляет собой сумму кинетической и потенциальной энернии:

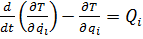(1)

— где 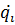– обобщенная скорость: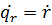

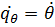
q_i – обобщенная скорость: q_r = r q_θ = θ

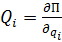– обобщенная сила

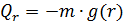
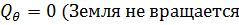
Запишем выражения кинетической энергии в полярных координатах

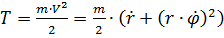(2)

Возьмем от (2) частные производные по 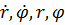и подставляем их в (1). Получаем уравнение движения ракеты на СУП:

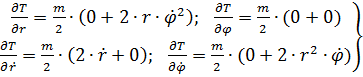(3)

Подставив (3) в (1) получаем:

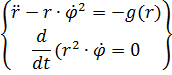
Решение этой параметрической системы приводится к координатной форме полярной СК:

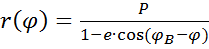(4)

Это уравнение конического сечения, где:

Р - фокальный параметр: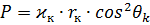

e – эксцентриситет: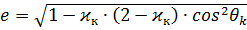

После преобразования уравнения конического сечения, изменим вид:

(5)

2.4. Расчет дальности полета

Найдем безразмерную скорость для нахождения фокального параметра и эксцентриситета:

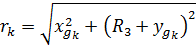
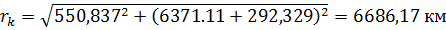
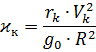
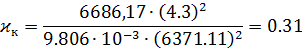
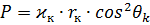
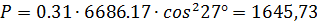
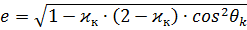
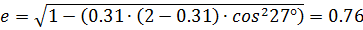
Находим дальность:

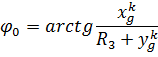
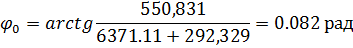
Полную угловую длину найдем из решения

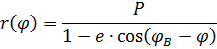
Полагая, что траектория пересекает Землю (r=R; φ =Ф_с)

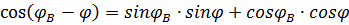
С учетом пересечения Земли (r=R; φ =Ф_с) определяем коэффициенты уравнения.