
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическая часть. Решение дифференциальных уравнений методом Эйлера
|
|
Лабораторная работа №2
Решение дифференциальных уравнений методом Эйлера
Разработала Куликова И.В. ассистент кафедры
«Высшая и прикладная математика»
Теоретическая часть
Метод Эйлера — наиболее простой численный метод решения обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление»[1]. Метод Эйлера является явным, одношаговым методом первого порядка точности, основанном на аппроксимации интегральной кривой кусочно-линейной функцией, т. н. ломаной Эйлера.
Пусть дана задача Коши для уравнения первого порядка
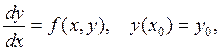 (1)
(1)
где функция f(x, y) определена на некоторой области  . Решение разыскивается на интервале [ x 0; b ]. На этом интервале введем узлы:
. Решение разыскивается на интервале [ x 0; b ]. На этом интервале введем узлы:
a = x 0< x 1< …< x i< …< x n= b, i =1, …, n, (2)
где xi =xi-1+ h, 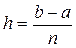 .
.
Приближенное решение в узлах, которое обозначим через определяется по формуле:
yi = yi -1+ f (xi -1, yi -1)× h. (3)