
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лабораторна робота №1. Мета: Навчитися ідентифікувати результати вимірювань з теоретичним розподілома, обчислювати математичне сподівання та СКВ.
|
|
Тема: ВИЗНАЧЕННЯ КООРДИНАТИ ЦЕНТРА РОЗПОДІЛУ ТА СЕРЕДНЬОКВАДРАТИЧНОГО (СКВ) ВІДХИЛЕННЯ РЕЗУЛЬТАТУ ВИМІРЮВАННЯ
Мета: Навчитися ідентифікувати результати вимірювань з теоретичним розподілома, обчислювати математичне сподівання та СКВ.
Теоретичні відомості.
Координату центру розподілу та СКВ результатів багатократних вимірювань визначають за допомогою середньоарифметичного, медіани та центру розмаху результатів.
Вибіркове середньоарифметичне приймають за незміщену оцінку центра будь-якого закону розподілу
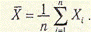
Середнє арифметичне є ефективною оцінкою результатів багатократних вимірювань для розподілів, близьких до нормального, але чутливе до наявності грубих похибок. Цього впливу частково позбуваються за допомогою оброблення 90 відсотків від обсягу добірки та вилучення з обох кінців варіаційного ряду X1 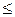 X2
X2 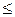 ...
... 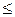 Xn no 5 відсотків найвіддаленіших результатів. Тоді отримують
Xn no 5 відсотків найвіддаленіших результатів. Тоді отримують
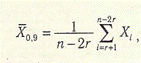
де 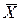 09 — середнє арифметичне 90 відсоткової добірки,
09 — середнє арифметичне 90 відсоткової добірки,
2 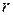 — кількість вилучених результатів вимірювань,
— кількість вилучених результатів вимірювань,
n — кількість результатів вимірювань.
Ефективною оцінкою центра експоненціальних пологоспадних одномодальних розподілів Лапласса з ексцесом 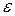 > 3, 8 є медіана варіаційного ряду вимірювань
> 3, 8 є медіана варіаційного ряду вимірювань
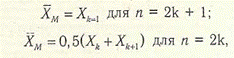
де 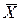 м — медіана середньоарифметичних значень вимірюваної фізичної величини.
м — медіана середньоарифметичних значень вимірюваної фізичної величини.
Для симетричних двомодальних розподілів з ексцесом 1 < 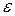
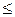 2, 4 ефективною є оцінка у вигляді середнього розмаху варіаційного ряду
2, 4 ефективною є оцінка у вигляді середнього розмаху варіаційного ряду
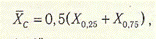
де 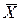 с — середній розмах варіаційного ряду;
с — середній розмах варіаційного ряду;
Х0.25 i X0.75 — відповідні 25 і 75 відсоткові квантілі.
Для обмежених розподілів з ексцесом 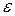 = 1, 0
= 1, 0 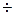 2, 4 центр розподілу оцінюють за допомогою центра розмаху варіаційного ряду
2, 4 центр розподілу оцінюють за допомогою центра розмаху варіаційного ряду
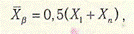
де 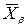 центр розмаху варіаційного ряду, що дуже чутливий до наявності грубих
центр розмаху варіаційного ряду, що дуже чутливий до наявності грубих
похибок.
Якщо закони розподілу невідомі, то за оцінку центра розподілу приймають медіану оцінок середньоарифметичного, середньоарифметичного 90 відсоткового, медіани середньоарифметичних значень вимірюваної фізичної величини, середнього розмаху та центру розмаху варіаційного ряду, розміщених у новий варіаційний ряд.
У разі невідомого математичного сподівання генерального середнього оцінку S2 генеральної дисперсії 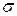 2 для будь-якого закону розподілу визначають, як
2 для будь-якого закону розподілу визначають, як

де S — статистична оцінка математичного сподівання,
S2 — статистична оцінка дисперсії теоретичного розподілу.
Для нормального закону розподілу за оцінку генерального СКВ результатів вимірювань приймають зміщену та асимптотично ефективну оцінку
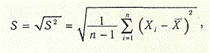
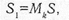
|
| а незміщену оцінку СКВ визначають, як |
де Mk — коефіцієнт, який для k від 1 до 60 відповідно дорівнює від 1, 253 до 1, 004.
Цим коефіцієнтом часто нехтують, а за СКВ результатів вимірювань беруть
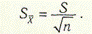
Приклад 1.
Дано результати 20 вимірювань розмірів А та частоти їх появи 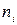 . Потрібно визначити оцінки результату вимірювань і СКВ.
. Потрібно визначити оцінки результату вимірювань і СКВ.