Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные схемы соединения трёхфазных цепей
|
|
Существуют различные способы соединения обмоток генератора с нагрузкой, но в целях экономии обмотки трёхфазного генератора соединяют в звезду или в треугольник.
 |
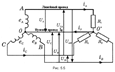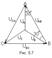
При соединении в звезду концы обмоток генератора объединяются в одну точку О, которая называется нулевой, или нейтральной (рис. 5.4).
Ниже приведены схемы соединения трёхфазного генератора с трёхфазной нагрузкой по схеме звезда: звезда с нулевым проводом (рис.5.5); звезда без нулевого провода (рис. 5.6).
 |
Точку, в которой объединяют три конца трёхфазной нагрузки при соединении её звездой, называют нулевой точкой нагрузки и обозначают О’.
Провода, соединяющие точки А, В, С генератора с точками а, b, с нагрузки, называют линейными.
Нулевым проводом называют провод, соединяющий нулевые точки генератора и нагрузки
Линейными токами Iл называют токи текущего линейным проводам (их обозначают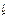 
, 
, 
)
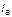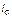Фазным напряжением Uф называют напряжение между началом и концом фазы или между линейным и нулевым проводом (их обозначают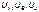 
).
Линейным напряжением UЛ называют напряжение между двумя линейными проводами (их обозначают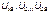 
).
Фазные и линейные напряжения связаны между собой выражениями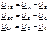 
. (5.4)
В симметричной системе фазных напряжений система линейных
напряжений тоже симметрична: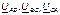 
равны по величине
и сдвинуты относительно друг друга на 1200 (рис. 5.7).
Действующее значение линейных напряжений легко определяется по векторной диаграмме (рис.5.7) из треугольника, например АОВ:
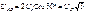. (5.5)
Таким образом, получим общее соотношение между линейными и фазными напряжениями в симметричной системе
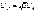. (5.6)
При соединении звездой в точках перехода из генератора в линию и из линии в нагрузку нет разветвлений, поэтому фазные и линейные токи одинаковы между собой в каждой фазе:
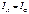. (5.6)
Запомните: соотношения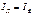 
, 
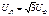справедливы только в звезде.
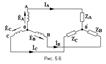
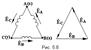При соединении обмоток генератора треугольником конец первой обмотки генератора соединяют с началом второй, конец второй с началом третьей, конец третьей- с началом пеhвой. (рис. 5.8)
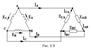
23.Геометрическая сумма Э.Д.С. в замкнутом треугольнике равна нулю (рис. 5.8). В отличие от соединения звездой, где в большинстве случаев применяется четырёхпроводная система, здесь используется три провода (рис. 5.9).
Соотношения между фазными и линейными токами легко можно определить, если для каждой узловой точки применить первый закон Кирхгофа:
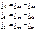; (5.7)
При симметричной нагрузке токи во всех фазах одинаковы: линейные токи сдвинуты относительно фазных токов на 900 (рис. 5.10).
Действующее значение линейных токов определяется по векторной диаграмме (рис.5.10) из треугольника, например АОС:
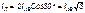. (5.8)
Таким образом, получим общее соотношение между линейными и фазными токами
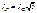. (5.9)
Из схемы (рис.5.9) видно, что фазные и линейные напряжения совпадают:
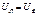. (5.10)
Запомните: соотношения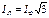 
; 
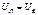справедливы только для треугольника
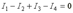
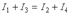запишем уравнение по первому закону Кирхгофа. 
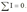Токам, направленным к узлу, присвоим знак " плюс", а токам, направленным от узла - знак " минус".
Согласно второму закону Кирхгофа, алгебраическая сумма ЭДС вдоль любого замкнутого контура равна алгебраической сумме падений напряжений в этом контуре 
Согласно закону Джоуля-Ленца, вся электрическая энергия, сообщаемая проводнику в результате работы сил электрического поля, превращается в тепловую энергию. С помощью закона Ома можно записать для потребителя с сопротивлением R: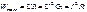 
Обычно под законом Джоуля-Ленца понимают уравнение, определяющее не энергию, а мощность тепловых потерь
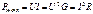В приведенных выражениях тепловая энергия и мощность выражаются в Джоулях [Дж]и Ваттах [Вт] соответственно.
4.Эквивалентность групп сопротивлений в линейных электрических цепях.
При последовательном соединении роль эквивалентного сопротивления (или сопротивления эквивалентного потребителя) играет сумма сопротивлений всех потребителей (рис. 1.11.).
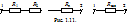
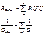Это следует из II закона Кирхгофа:
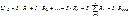При двух последовательно соединенных потребитлях:
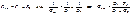При параллельном соединении роль эквивалентной проводимости (или проводимости эквивалентного потребителя) играет сумма проводимостей всех потребителей (рис. 1.12.).
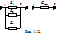
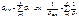Это следует из I закона Кирхгофа:
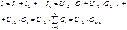При двух параллельно соединенных потребителях
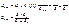Таким образом, для расчета цепей с последовательно включенными потребителями целесообразно их свойства выражать значениями сопротивлений, а для параллельно включенных – значениями проводимостей.
14. Последовательное соединение элементов R, L, C в цепи синусоидального напряжения
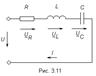В электрической цепи (рис. 3.11) элементы R, L, C соединены последовательно и подключены к источнику синусоидального напряжения. Ток в такой цепи будет изменяться также по синусоидальному закону.
Все законы постоянного тока справедливы и для синусоидального, только записанные в комплексной форме.
Вектор напряжения на входе равен сумме векторов напряжений на элементах R, L, C:
. (3.27)
По закону Ома можно расписать:
.
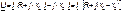Отсюда
. (3.28)
Значит полное сопротивление для цепи на рис. 3.11
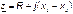, (3.29)
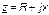, (3.30)
где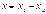 
- реактивное сопротивление электрической цепи.
Можно рассмотреть три случая значений:
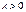, значит 
;
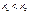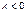, значит 
;
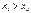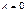, значит 
.
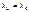15. Парралельное соединение R, L, C
. Параллельное соединение резистивного и емкостного элементов
Для цепи на рис. 18 имеют место соотношения:
;
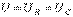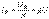, где 
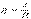[См] – активная проводимость;
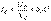, где 
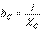[См] – реактивная проводимость конденсатора
Параллельное соединение резистивного и индуктивного элементов
Для цепи на рис. 21 можно записать
;
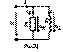
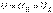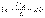, где 
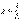[См] – активная 
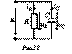проводимость;
, где 
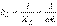[См] – реактивная проводимость катушки индуктивности.
.
20.Последовательное соединение индуктивно связанных элементов цепи
 |
Две катушки с сопротивлениями R1 и R2, индуктивностями L1 и L 2 и взаимной индуктивностью М соединены последовательно. Возможны два вида их включения: согласное (рис. 4.4а) и встречное (рис. 4.4б).
При согласном включении токи в обоих элементах в любой момент времени направлены одинаково относительно одноименных выводов, поэтому магнитные потоки самоиндукции Ф11 (или Ф22 ) и взаимной индукции Ф12 (или Ф21 ), сцепленные с каждым элементом, складываются. При встречном включении токи в обоих элементах цепи в любой момент времени направлены противоположно относительно одноименных выводов, поэтому магнитные потоки самоиндукции и взаимной индукции, сцепленные с каждым элементом, вычитаются.
Индуктивность двух последовательно соединенных индуктивно связанных элементов определяется выражением:
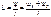, (4.7)
где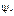 
и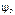 
- потокосцепления первого и второго элементов, причем 
; 
.
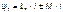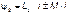Знак плюс относится к согласному, а знак минус ко встречному включению. Следовательно,
L = L1 + L2 ± 2M.
Полное сопротивление при согласном включении больше, чем при встречном.
Напряжения на элементах имеют по три составляющие:
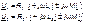(4.8)
Если индуктивность одного из элементов меньше взаимной индуктивности, то при встречном включении наблюдается своеобразный «емкостный» эффект. Пусть, например, L2 < М, при этом в выражении
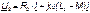
имеем ω (L2-M) < 0, и, следовательно, напряжение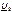 
отстает по фазе от тока 
, как в случае емкостного сопротивления. Конечно, реактивное сопротивление всей цепи в целом индуктивное, так как L = L1+ L2 - 2М > 0 и ток отстает по фазе от напряжения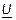 
.